Jtdcftul

本条目部分链接不符合格式手冊規範。跨語言链接及章節標題等處的链接可能需要清理。（2015年12月11日） 請協助改善此條目。參見WP:LINKSTYLE、WP:MOSIW以了解細節。突出显示跨语言链接可以便于检查。

  本文介绍拓扑学中的商空间，线性代数中的商空间参见商空间。

在拓扑学及其相关数学领域，一个商空间（quotient space，也称为等化空间identification space）直观上说是将一个给定空间的一些点等同或“黏合在一起”；由一个等价关系确定哪些点是等同的。这是从给定空间构造新空间的常见方法。

定义

假设X是一个拓扑空间，~是X上一个等价关系。我们在商集合X/~（这个集合有所有~的等价类组成）上定义一个拓扑如下：X/~中一个等价集合是开集当且仅当他们的并集在X中是开集。所得的拓扑称为在商集合X/~上的商拓扑（quotient topology）。

等价地，商拓扑可以如下方式刻画：设q : X → X/~是投影映射，将X的任何元素映为它的等价类。则X/~上的商拓扑是使q 连续的最细拓扑（finest topology）。

给定一个满射f : X → Y从一个拓扑空间X到一个集合Y，我们可以在Y上定义商拓扑为使f连续的最细拓扑。这等价于说集合V ⊆ Y在Y中开当且仅当它的原像f⁻¹(V)在X中开。映射f在X上诱导了一个等价关系，即x₁~x₂当且仅当f(x₁) = f（x₂）。这个商空间X/~ 同胚于Y（带着它的商拓扑），同构映射为将x的等价类映为f(x)。

一般地，一个满连续映射f : X → Y称为一个商映射（quotient map）如果Y具有由f确定的商拓扑。

例子

• 
  黏合：通常，拓扑学家讨论将一些点黏合在一起。如果X是一个拓扑空间，点x,y∈X{displaystyle x,yin X}“黏合”在一起，这意味着我们考虑由等价关系a~b当且仅当a = b或a = x, b = y（或a = y, b = x）得到的商空间。即这两个点被看作一个。


• 考虑一个单位正方形I² = [0,1]×[0,1]以及由所有边界点等价生成的等价关系~，从而所有边界点等同到一个等价类。则I²/~同构于单位球面S²。


• 
  黏着空间（Adjunction space）：更一般地，假设X是一个空间，A是X的一个子空间。我们可以将A中所有点等同到一个等价类，而A以外的点不变。所得的空间记作X/A。2维球面同构于将单位圆盘的边界等同为一个点D²/∂D²。


• 考虑集合X = R'，取通常拓扑的实数集，记x ~ y 当且仅当x−y是一个整数。则商空间X/~同构于单位圆周S¹，同构映射为将x的等价类映为 exp（2πix）。


• 上一个例子的一类大量的推广如下：假设一个拓扑群G连续作用在空间X上。我们可以构造X上一个等价关系，如果两点等价当且仅当它们在同一个轨道中。这个关系下的商空间称为轨道空间，记作X/G。上一个例子中G = Z通过平移作用在R上。轨道空间 R/Z同构于S¹。

注：记号R/Z有歧义：如果Z理解成一个群作用在R上则商空间是圆周；如果Z看作R的一个子空间，则商空间是无穷的一束圆（bouquet of circles）在同一个点联接起来。

性质

商映射 q : X → Y是由如下性质刻画的满射：如果Z是任何拓扑空间，f : Y → Z是任何函数，则f连续当且仅当f O q连续。

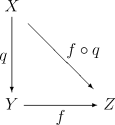
商空间X/~与商映q : X → X/~一起由如下泛性质刻画。如果g : X → Z是一个连续映射使得：对所有a与b属于X，a~b蕴含g(a)=g(b)，则存在惟一连续映射f : X/~ → Z使得g = f O q。我们称 g“下降到商”。

因此定义在X/~商的连续映射恰是由定义在X上与等价关系一致的连续映射（它们将同一个等价类中的元素映到相同的像）诱导的。在研究商空间时，时常使用这个判据。

给定一个连续满射f : X → Y，关于f是否为商映射的判据是有用的。两个充分条件是f为开映射或闭映射。注意这两个条件只是充分条件而不是必要的。容易构造出不开或不闭的商映射例子。

与其它拓扑概念的相容性

• 
  分离
  
  
  
  • 一般地，商空间关于分离公理的表现都很坏。X的分离性质不必被X/~继承，而X/~可能具有X所没有的分离性质。
  
  
  • 
    X/~是一个T1空间当且仅当~的任何等价类在X中闭。
  
  
  • 如果商映射开则X/~是一个豪斯多夫空间当且仅当~是乘积空间X×X的一个子集。
  
  
  
  


• 
  连通性
  
  
  
  • 如果一个空间是连通的或道路连通，则所有的商空间也是。
  
  
  • 一个单连通或可缩空间的商空间不必具有同样的性质。
  
  
  
  


• 
  紧性
  
  
  
  • 如果一个空间紧，则所有商空间也是。
  
  
  • 一个局部紧空间的商空间不必是局部紧的。
  
  
  
  


• 
  维数
  
  • 一个商空间的拓扑维数可能比原空间大（顯然也可能比較小），皮亚诺曲线（space-filling curve）提供了这样的例子。
  
  

又见

拓扑学

• 子空间


• 乘积空间


• 不交并


• 
  最终拓扑（Final topology）

代数

• 商群


• 商空间


• 商范畴

参考

• Stephen Willard, General Topology, (1970) Addison-Wesley Publishing Company, Reading Massachusetts.


• 
  PlanetMath上Quotient space的資料。