正六邊形鑲嵌
| 正六邊形鑲嵌 | |
|---|---|
 (點選檢視大圖) | |
| 類別 | 正鑲嵌 |
| 頂點圖 | 6.6.6 (or 63) |
| 頂點佈局 | 63 |
| 考克斯特符號 | |
| 施萊夫利符號 | {6,3} t0,1{3,6} |
| 威佐夫符號 | 3 | 6 2 2 6 | 3 3 3 3 | |
| 康威表示法 | H |
| 對稱群 | p6m, [6,3], (*632) |
| 對偶 | 正三角形鑲嵌 |
| 旋轉對稱群 | p6, [6,3]+, (632) |
| 二面角 | 180度(平角) |
 6.6.6 (or 63) (頂點圖) | |
 正三角形鑲嵌 (對偶多面體) | |
在幾何學中,正六邊形鑲嵌是一種平面鑲嵌,由正六邊形重覆組合排列而成,且填滿整個平面,而且沒有任何空隙或重疊,由於皆由正多邊形組成,因此稱為正鑲嵌圖。正六邊形鑲嵌是三维欧几里得空间中三个正密铺之一。另外两个分别是正三角形镶嵌和正方形镶嵌。
由於正六邊形鑲嵌是由正六邊形組成,又因正六邊形內角為120°,因此每個頂點周圍都有3個正六邊形,且剛好占滿360°,才能填滿平面。
在施萊夫利符號中,正六邊形鑲嵌可用{6,3}或t{3,6}表示。
目录
1 圆堆砌
2 半正涂色
3 相关半正镶嵌
4 基于正六边形镶嵌和正三角形镶嵌的Wythoff构建
5 拓扑相同的镶嵌
6 應用
7 參考文獻
圆堆砌
正六边形镶嵌可以被用来进行圆堆砌,以其每个顶点为圆心放置等直径的圆。在这个堆砌里,每个圆都与3个相邻圆接触(接触数)。每个正六边形中间的部分实际上还可以再放入一个圆,这样我们就会得到二维最密圆堆砌——正三角形镶嵌式圆堆砌,这时接触数达到最大值6。
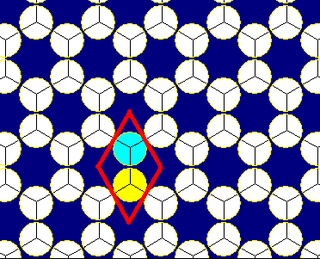
半正涂色
正六边形镶嵌共有3种不同的半正涂色,都可以由Wythoff镜面对称构造出来。(h,k)表示一种涂色的面周期性重复,以正六边形距离h、k计数,h在先,k在后。
| k阶半正 | 一阶半正 | 二阶半正 | 三阶半正 | ||||
|---|---|---|---|---|---|---|---|
| 图像 |  |  |  |  |  |  |  |
| 颜色数 | 1 | 2 | 3 | 2 | 4 | 2 | 7 |
| (h,k) | (1,0) | (1,1) | (2,0) | (2,1) | |||
施莱夫利符号 | {6,3} | t{3,6} | t0,1,2{3[3]} | ||||
Wythoff符号 | 3 | 6 2 | 2 6 | 3 | 3 3 3 | | ||||
对称性 | *632 (p6m) [6,3] | *333 (p3) [3[3]] | *632 (p6m) [6,3] | 632 (p6) [6,3]+ | |||
考克斯特符号 | |||||||
康威多面体符号 | H | tH | teH | t6daH | t6dateH | t6dsH | |
其中三色正六边形镶嵌是一个由三阶全序多胞形产生的镶嵌。
相关半正镶嵌
正六边形镶嵌可以通过截角操作得到一系列与之相关的半正镶嵌,其与正六边形镶嵌拥有相似的对称性:
对称性: [6,3], (*632) | [6,3]+, (632) | [1+,6,3], (*333) | [6,3+], (3*3) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |  |  | |
{6,3} | t0,1{6,3} | t1{6,3} | t1,2{6,3} | t2{6,3} | t0,2{6,3} | t0,1,2{6,3} | s{6,3} | h{6,3} | h1,2{6,3} | |
| 半正对偶 | ||||||||||
 |  |  |  |  |  |  |  |  | ||
V6.6.6 | V3.12.12 | V3.6.3.6 | V6.6.6 | V3.3.3.3.3.3 | V3.4.12.4 | V.4.6.12 | V3.3.3.3.6 | V3.3.3.3.3.3 | ||
正六边形镶嵌在拓扑上与一系列一直延伸到双曲镶嵌的顶点图为n3的(广义)多面体相关:
多面体 | 欧式镶嵌 | 双曲镶嵌 | ||||||
|---|---|---|---|---|---|---|---|---|
 {2,3} |  {3,3} |  {4,3} | {5,3} |  {6,3} |  {7,3} |  {8,3} | ... |  {∞,3} |
(三阶)正六边形镶嵌在拓扑上与一系列面为正六边形的密铺相关联,这些镶嵌都可称之为“正六边形镶嵌”,所以我们以“n 阶”来区分,其施莱夫利符号为{6,n},考克斯特符号![]()
![]()
![]()
![]()
![]() ,一直到n = ∞:
,一直到n = ∞:
| 球面 | 欧氏 | 双曲镶嵌 | ||||||
|---|---|---|---|---|---|---|---|---|
 {6,2} |  {6,3} |  {6,4} |  {6,5} |  {6,6} |  {6,7} |  {6,8} | ... |  {6,∞} |
这个镶嵌还是一系列有考克斯特对称群[n,3]对称性的(半)截角菱形多面体或镶嵌的一员。立方体可以被看作是“菱形六面体”,这里菱形就是正方形。它们的截角形在原顶点处有正的多边形,而原来的菱形面则被截成了非正六边形。这一系列多面体或镶嵌有两种顶点图:(n.6.6)和(6,6,6)。
| 多面体 | 欧氏镶嵌 | 双曲镶嵌 | |||
|---|---|---|---|---|---|
| [3,3] | [4,3] | [5,3] | [6,3] | [7,3] | [8,3] |
 立方体 |  菱形十二面体 | 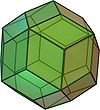 菱形三十面体 |  菱形镶嵌 |  |  |
 倒角四面體 |  倒角立方體 |  倒角十二面體 |  正六邊形鑲嵌 | ||
正六边形镶嵌亦可被看作延长菱形镶嵌,菱形镶嵌的每一个顶点都被延长成了新的棱。这类似于三维空间中的菱形十二面体堆砌和菱形六角化十二面体堆砌之间的关系。
 菱形镶嵌 |  正六边形镶嵌 |  利用这一关系的栅栏 |
基于正六边形镶嵌和正三角形镶嵌的Wythoff构建
就像半正多面体一样,这里也有8个基于正六边形镶嵌(和正三角形镶嵌)的半正镶嵌。在以下的图片中,原有面对应的面被涂成了红色,原有顶点所对应的面被涂成了黄色,原有棱对应的面被涂成了蓝色。这8个半正镶嵌中,只有7个是拓扑上相异的。(截顶正三角形镶嵌与正六边形镶嵌在拓扑上相同)
对称性: [6,3], (*632) | [6,3]+ (632) | [1+,6,3] (*333) | [6,3+] (3*3) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
{6,3} | t{6,3} | r{6,3} r{3[3]} | t{3,6} t{3[3]} | {3,6} {3[3]} | rr{6,3} s2{6,3} | tr{6,3} | sr{6,3} | h{6,3} {3[3]} | h2{6,3} r{3[3]} | s{3,6} s{3[3]} |
= | = | = | = | |||||||
| 半正对偶 | ||||||||||
V63 | V3.122 | V(3.6)2 | V63 | V36 | V3.4.12.4 | V.4.6.12 | V34.6 | V36 | V(3.6)2 | V36 |
| 三角形 对称性 | 拓展对称性 | 拓展 符号 | 拓展 阶 | 堆砌符号 |
|---|---|---|---|---|
| a1 | [3[3]] | ×1 | (None) | |
| i2 | <[3[3]]> = [6,3] | = | ×2 | |
| r6 | [3[3[3]]] = [6,3] | = | ×6 |
Wythoff | 3 | 3 3 | 3 3 | 3 | 3 | 3 3 | 3 3 | 3 | 3 | 3 3 | 3 3 | 3 | 3 3 3 | | | 3 3 3 |
|---|---|---|---|---|---|---|---|---|
考克斯特 | ||||||||
| 图像 顶点图 |  (3.3)3 |  3.6.3.6 |  (3.3)3 |  3.6.3.6 |  (3.3)3 |  3.6.3.6 |  6.6.6 | 3.3.3.3.3.3 |
拓扑相同的镶嵌
正六边形镶嵌是有着{6,3}拓扑的一种特殊的正的镶嵌,而实际上,这里有12种类型的非正但是面全同且顶点全同的六边形镶嵌,前7种可以被认为是没有边对边正好对上的四边形镶嵌,也可被认为是有两对共线边的六边形镶嵌。这里的“对称性”假定所有的面都是相同的。

平行四边形
p2对称

平行四边形
pmg对称

平行四边形
pgg对称

矩形
pgg对称

梯形
pmg对称

矩形
pgg对称

矩形
cmm对称

六边形
p2对称

六边形
pgg对称

六边形
pmg对称

展长六边形
cmm对称

正六边形
p6m对称
正六边形镶嵌也可被变形为一种手征性的四填充色三向同性的编织图案。其中部分正六边形被扭曲成了平行四边形。这一图案有着旋转632 (p6) 对称性。
| 正六边形 | 六边形编织 |
|---|---|
| p6m (*632) | p6 (632) |
 |  |
應用
正六邊形鑲嵌是二維空間最密的排列方式。在蜂窩猜想中,正六邊形鑲嵌是使用最少的總周長將該表面劃分成面積相等的區域的最佳方法。[1][2]最佳的三維結構由開爾文勳爵(Lord Kelvin)提出,他認為,開爾文結構(體心立方晶格)是最佳的結構(最佳結構可能出現於肥皂泡)。然而,一个更加不对称的威尔-费兰结构要比它好一些。
维基共享资源中相关的多媒体资源:正六邊形鑲嵌 |
參考文獻
^
Weisstein, Eric W. Honeycomb Conjecture. MathWorld. [27 Dec 2010].
^
Hales, Thomas C. The Honeycomb Conjecture. Discrete and Computational Geometry. 8 Jun 1999, 25: 1–22 (2001). arXiv:math/9906042.
.mw-parser-output .refbegin{font-size:90%;margin-bottom:0.5em}.mw-parser-output .refbegin-hanging-indents>ul{list-style-type:none;margin-left:0}.mw-parser-output .refbegin-hanging-indents>ul>li,.mw-parser-output .refbegin-hanging-indents>dl>dd{margin-left:0;padding-left:3.2em;text-indent:-3.2em;list-style:none}.mw-parser-output .refbegin-100{font-size:100%}
Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p. 296, Table II: Regular honeycombs
Grünbaum, Branko ; and Shephard, G. C. Tilings and Patterns. New York: W. H. Freeman. 1987. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p. 58-65)
埃里克·韦斯坦因. Hexagonal Grid. MathWorld.
- 埃里克·韦斯坦因. Regular tessellation. MathWorld.
- 埃里克·韦斯坦因. Uniform tessellation. MathWorld.
- Richard Klitzing, 2D Euclidean tilings, o3o6x - hexat - O3
Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979: 35. ISBN 0-486-23729-X.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1]
| ||||||||||||||||||
| ||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||











