参考系
参考系(又称参照系、参考坐标),在物理學中指用以測量並記錄位置、定向以及其他物體屬性的坐標系;或指與觀測者的運動狀態相關的觀測參考系;又或同指兩者。
目录
1 各種參考系
1.1 坐標系
1.2 觀測者參考系
1.3 量度儀器
2 慣性參考系
2.1 備註
3 非慣性參考系
4 常用的特定參考系
5 參見
6 注释
7 参考文献
8 外部連結
各種參考系
參考系有許多種,所以在提到參考系時,常會在前面加上字詞指定是哪一種參考系,如笛卡儿坐标系。人們也會指定參考系的屬性:旋轉參考系強調參考系的運動狀態,伽利略參考系強調系與系之間的變換法,而宏觀或微觀參考系則強調參考系的尺度大小。[註 1]
在本條目中,「觀測者參考系」強調的是運動的狀態,而非某種特定坐標系的選擇,或是用於觀測的儀器。這種用法能夠研究觀測者的運動對坐標系的影響,無論觀測者使用的坐標系是哪一種。另一方面,當觀測者的運動狀態並非主要的針對點時,不同的「參考系」能夠利用不同系統的對稱性,來簡化計算的過程。更廣義的來說,許多物理學中的問題都用到廣義坐標、實模態或特徵向量,這些都和時間和空間沒有直接的關係。下文因此有必要分開敘述各種參考系,把觀測者參考系、坐標系及觀測儀器作為獨立的概念來看,如下:
- 觀測者參考系(如慣性參考系或非慣性參考系)是與運動狀態有關的物理概念。
- 坐標系為一個數學概念,是用於描述物理問題一種語言[註 2]。所以,在一個觀測者參考系中的觀測者可以選用各種各樣的坐標系(笛卡爾坐標系、極坐標系、曲線坐標系、廣義坐標系等等)來描述從該參考系中觀測到的現象。坐標系的改變並不影響觀測者本身的運動,也就不會影響這個觀測者的「觀測者參考系」[4]。某一些坐標系比另一些更適合描述特定的物理問題,在同一個觀測者參考系中,可以任選其一。
- 對量度或觀測工具的選擇獨立於觀測者的運動狀態和其選用的坐標系。
坐標系
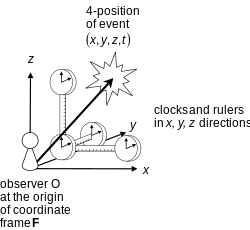
觀測者O位於一組坐標(參照系F)的原點。該參照系使用的本地坐標(x, y, z, t)來表示時空事件(以星形表示)。
「坐標」一詞的意義有時是非專業性的(特別在物理學中),然而它在數學中卻具有準確的意義。
數學中的坐標系是一個幾何學和代數學用到的概念[5][6],一般作為流形的一種特性(如物理學中的位形空間和相空間)[7][8]。一個點r在n維空間中的坐標表達方式為n-元組:[9][10]
- r=[x1, x2, … ,xn] .{displaystyle mathbf {r} =[x^{1}, x^{2}, dots ,x^{n}] .}
在廣義的巴拿赫空間中,這些數字能夠是諸如傅立葉級數等函數展開式中的系數。在物理問題中,它們可以是時空坐標或實模態振幅。當用在機器人設計時,它們可以是相對旋轉的角度、直線平移或關節的變形度等[11]。在此我們假設這些坐標能夠以笛卡爾坐標系中的一組函數表示:
xj=xj(x, y, z, …) ,{displaystyle x^{j}=x^{j}(x, y, z, dots ) ,} j=1, … , n {displaystyle j=1, dots , n }
其中x、y、z等等為該點的n個笛卡爾坐標數。給定這些函數,定義坐標面為以下關係:
xj(x,y,z,…)={displaystyle x^{j}(x,y,z,dots )=} 常數 j=1, … , n .{displaystyle j=1, dots , n .}
這些面的相交處定義為坐標線。在任何一點上,與相交的坐標線相切的所有切線組成一組在那一點的基向量:{e1, e2, …, en}。也就是:[12]
- ei(r)=limϵ→0r(x1, …, xi+ϵ, …, xn)−r(x1, …, xi, …, xn)ϵ ,{displaystyle mathbf {e} _{i}(mathbf {r} )=lim _{epsilon rightarrow 0}{frac {mathbf {r} left(x^{1}, dots , x^{i}+epsilon , dots , x^{n}right)-mathbf {r} left(x^{1}, dots , x^{i}, dots , x^{n}right)}{epsilon }} ,}
這能夠歸一化為單位長度。
坐標面、坐標線以及基向量組成一個坐標系[13]。如果基向量在每一點上都兩兩正交,則該坐標系稱為正交坐標系。
坐標系中一個重要的方面在於其度量gik,它在坐標系中以一組坐標表達弧長ds:[14]
- (ds)2=gik dxi dxk ,{displaystyle (ds)^{2}=g_{ik} dx^{i} dx^{k} ,}
並求和所有重復的索引。
根據上文可以看出,參考系其實是一個數學模型,屬於公理系統的一部分。參考系和物體運動實際上並沒有關係,但在加上時間作為又一個坐標後,它就能夠描述運動。所以,洛倫茲變換及伽利略變換可以被視為坐標轉換。
觀測者參考系

狹義相對論中的三個參考系。黑色的為靜止的。帶撇號的參考系以光速的40%速度運行,帶兩個撇號的則以光速的80%運行。注意當速度提升時,坐標線呈剪刀狀變動。
觀測者參考系,或一般只稱為參考系,是與觀測者以及其運動狀態相關的物理概念。在本文中所指的,是只和運動狀態有關的參考系[15]。不過,人們對此觀點並无共識。在狹義相對論中,「觀測者」和「參考系」一般是有分別的。這一觀點認為,參考系是觀測者加上一個右手正交坐標系,該坐標系由一組正交的空間向量和與其垂直的一個時間向量組成[16]。本文並不使用這種狹義的觀點[17][18]。在廣義相對論中,廣義坐標系的使用是很常見的(參見獨立球體外的引力場的史瓦西解[19])。
觀測者參考系有兩種:慣性與非慣性參考系。慣性參考系中的物理定律都處於最為簡單的形式。在狹義相對論中,這種參考系通過洛倫茲變換相互變換,其參數為快度。在牛頓力學中,慣性參考系定義為牛頓第一定律必須成立的參考系,也就是在這種參考系中的自由粒子要麼以直線恒速運行,要麼保持靜止。它們之間以伽利略變換互相轉換。
與之相對的是非慣性參考系,當中的物理現象必須用到假想力才能解釋。其中一個例子為位於地球表面的參考系。該參考系圍繞地球中心旋轉,因此造成一系列的假想力,如科里奧利力、離心力和引力。(這些力,包括引力在內,都是在真正的慣性參考系——自由落體——中不存在的。)
量度儀器
參考系的其中一方面在於,加載與參考系上的量度儀器有關的(如鐘或長桿等)到底具有甚麼樣的角色。本文不討論這一問題,而這是在量子力學中牽涉到觀測者與測量之間關係的一個課題。
在物理實驗中,實驗室量度儀器靜止位處的參考系稱為實驗室參考系。某些實驗中的實驗室參考系是慣性參考系,而另一些則不是(如在地球表面的大部分實驗室都是非慣性參考系)。在粒子物理學中,一個常見的做法是把實驗室參考系中的能量與動量轉換到質心系中,這樣可以簡化計算過程。
在思想實驗中用到的鐘或長桿等觀測者的量度儀器,在實際實驗中是以非常複雜的儀器取代,從而間接地做出測量的。這些儀器用到真空的屬性,其原子鐘根據標準模型運作,時間也必須根據引力時間膨脹做出調整[20]。
其實,愛因斯坦認為鐘和長桿應該由更基礎的物體取代,如原子和分子等[21]。
慣性參考系
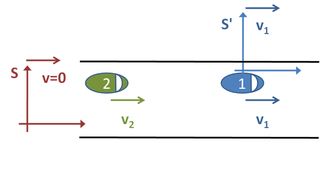
兩輛車以不同的均速移動,S為固定在路面的慣性參考系,而S' 為固定在第一輛車上的慣性參考系。
兩輛車以不同的均速在路面行駛(見圖)。在某一時刻,它們間隔200米。前方的那輛車以每秒22米的速度行駛,隨後的那輛車以每秒30米的速度行駛。要計算第二輛車在多久後會趕上第一輛車,我們可以使用三個參考系的其中一個。
首先,我們可以從路邊觀測兩輛車。定義路邊的參考系為S:計時器在第二輛車經過路邊觀測者時開始,這時兩車相距d = 200 m。兩輛車都以均速運行,所以我們可以用以下的公式表述它們的位置:x1(t){displaystyle x_{1}(t)}為第一輛車在時間t秒後的位置,而x2(t){displaystyle x_{2}(t)}為第二輛車在時間t秒後的位置。
- x1(t)=d+v1t=200 + 22t ;x2(t)=v2t=30t{displaystyle x_{1}(t)=d+v_{1}t=200 + 22t ;quad x_{2}(t)=v_{2}t=30t}
當時間為t = 0 s時,第一輛車位於200米處,而第二輛車位置為零,這符合實際情況。我們要設 x1=x2{displaystyle x_{1}=x_{2}},並求t{displaystyle t}:
- 200+22t=30t{displaystyle 200+22t=30tquad }
- 8t=200{displaystyle 8t=200quad }
- t=25s{displaystyle t=25quad mathrm {s} }
或者我們可以選擇位於第一輛車上的參考系S' 。在這個參考系裏,第一輛車是靜止的,而第二輛車跟隨在後,速度為v2 − v1 = 8 m / s。趕上前一輛車所需的時間為d /( v2 − v1) = 200 / 8 s,也就是25秒,同上。使用這個參考系比上一個參考系簡單得多。第三種做法是,取位於第二輛車上的參考系。這和以上的例子相似,但這次第二輛車為靜止,而第一輛車以每秒8米的速度向後退。
另外我們也可以使用旋轉或加速的參考系,但這樣會不必要地把問題複雜化了。值得注意的是,在任何參考系中作出的測量都可以換算成其他的參考系。
備註
以上的例子作了一些假設。比如牛頓使用的是世界時,因此兩個相互以高速均速運動的鐘的時間流逝率永遠是一樣的。他認為一個參考系中的時間流逝率應該和所有其他參考系中的一樣。也就是說,所有參考系的時間流逝率都和一個絕對的世界時相同,並不取決於參考系的位置和速率。愛因斯坦於1905年在他的狹義相對論中延伸了這一概念,並假設所有物理定律在所有的慣性參考系中都相同(包括光在真空中的速度),在這種原理下參考系之間的變換方法稱為洛倫茲變換。
另外,慣性參考系的定義並不局限於三維歐幾里得空間。牛頓所用的為簡單的歐幾里得空間,但廣義相對論則用一種更為廣義的幾何。就拿橢球體的幾何為例,其中的自由粒子定義為沿著測地線均速移動或靜止不動。兩個自由粒子可以在表面上的同一點開始,以均速向不同方向運行。一段時間後,兩個粒子會在橢球體的另一邊會和相撞。粒子均以均速運行,符合沒有外在施力的定義;沒有加速度,也就符合了牛頓第一定律。因此這兩個粒子位於慣性參考系當中。它們最後的相撞是橢球體的幾何造成的。類似地,人們現在相信存在一種稱為時空的四維幾何,而這種幾何能夠解釋為甚麼兩個有質量的物體在沒有外力的情況下會互相靠近。時空的曲率取代了牛頓力學和狹義相對論中的引力。
非慣性參考系
非慣性參考系和慣性參考系之間的分別在於,在用到非慣性參考系時,必須用到假想力。
加速參考系一般以撇號標記,所有與其相關的變量都加以撇號:x' 、y' 、a' 等。
某慣性參考系和非慣性參考系之間的距離一般記為R。取同時存在於兩個參考系中的任意點,從慣性參考系原點指向該點的向量長度為r,而從非慣性參考系原點指向該點的向量長度為r'。以下的關係成立:
- r=R+r′{displaystyle mathbf {r} =mathbf {R} +mathbf {r} '}
取一階及二階導數後得:
- v=V+v′{displaystyle mathbf {v} =mathbf {V} +mathbf {v} '}
- a=A+a′{displaystyle mathbf {a} =mathbf {A} +mathbf {a} '}
其中V和A分別為相對非慣性參考系的速率和加速度,而v和a分別為相對慣性參考系的速率和加速度。
利用這些公式,我們能夠在兩種參考系之間變換。比如,牛頓第二定律現在可以寫作:
- F=ma=mA+ma′{displaystyle mathbf {F} =mmathbf {a} =mmathbf {A} +mmathbf {a} '}
當從旋轉參考系等加速參考系來看時,慣性似乎表現為一種力(旋轉參考系中有離心力及與垂直於物體移動路徑的科里奧利力)。
其中一種常見的加速參考系為同時旋轉並平移的參考系(如固定在搬動並運作中的播放機裏的光碟上的參考系)。如此的參考系有以下的方程:
- a=a′+ω˙×r′+2ω×v′+ω×(ω×r′)+A0{displaystyle mathbf {a} =mathbf {a} '+{dot {boldsymbol {omega }}}times mathbf {r} '+2{boldsymbol {omega }}times mathbf {v} '+{boldsymbol {omega }}times ({boldsymbol {omega }}times mathbf {r} ')+mathbf {A} _{0}}
或求相對加速參考系的物體加速度:
- a′=a−ω˙×r′−2ω×v′−ω×(ω×r′)−A0{displaystyle mathbf {a} '=mathbf {a} -{dot {boldsymbol {omega }}}times mathbf {r} '-2{boldsymbol {omega }}times mathbf {v} '-{boldsymbol {omega }}times ({boldsymbol {omega }}times mathbf {r} ')-mathbf {A} _{0}}
兩邊乘以質量m得
- F′=Fphysical+FEuler′+FCoriolis′+Fcentripetal′−mA0{displaystyle mathbf {F} '=mathbf {F} _{mathrm {physical} }+mathbf {F} '_{mathrm {Euler} }+mathbf {F} '_{mathrm {Coriolis} }+mathbf {F} '_{mathrm {centripetal} }-mmathbf {A} _{0}}
其中
FEuler′=−mω˙×r′{displaystyle mathbf {F} '_{mathrm {Euler} }=-m{dot {boldsymbol {omega }}}times mathbf {r} '}(歐拉力)
FCoriolis′=−2mω×v′{displaystyle mathbf {F} '_{mathrm {Coriolis} }=-2m{boldsymbol {omega }}times mathbf {v} '}(科里奧利力)
Fcentrifugal′=−mω×(ω×r′)=m(ω2r′−(ω⋅r′)ω){displaystyle mathbf {F} '_{mathrm {centrifugal} }=-m{boldsymbol {omega }}times ({boldsymbol {omega }}times mathbf {r} ')=m(omega ^{2}mathbf {r} '-({boldsymbol {omega }}cdot mathbf {r} '){boldsymbol {omega }})}(離心力)
常用的特定參考系
- 國際地表參考系統
- 國際天球參考系統
參見
- 分析力學
- 工程力學
- 笛卡爾坐標系
- 離心力
- 向心力
- 經典力學
- 科里奧利力
- 曲線坐標系
- 圓柱坐標系
- 動力學
- 假想力
- 弗萊納公式
- 伽利略不變性
- 伽利略變換
- 廣義相對論
- 廣義坐標
- 廣義力
- 慣性參考系
- 運動學
- 洛倫茲變換
- 馬赫原理
- 正交坐標系
- 相對性原理
- 狹義相對論
- 球坐標系
- 相對論
- 圓環坐標系
注释
^ 例如在電磁學裏,不同時間與長度尺度的本構關係用於判斷代入麥克斯韋方程組的電流與電荷的量[1]。這些宏觀與微觀參考系的分別在熱力學中也有出現[2]。
^ 在數學中,最廣義的坐標系是複李群中弧xi = xi (t)的集合。見:Lev Semenovich Pontri͡agin. L.S. Pontryagin: Selected Works Vol. 2: Topological Groups 3rd Edition. Gordon and Breach. : 429. ISBN 2-88124-133-6. 引文格式1维护:冗余文本 (link)。不那麼抽象地說,n維空間中的坐標系定義為一組基向量的集合{e1, e2,… en} [3]。因此,坐標系是一個數學中建立的概念,有時候但不一定和物體的實際運動有直接的關係。
参考文献
^ Kurt Edmund Oughstun. Electromagnetic and Optical Pulse Propagation 1: Spectral Representations in Temporally Dispersive Media. Springer. 2006: 165. ISBN 0-387-34599-X.
^ Paul McEvoy. Classical Theory. MicroAnalytix. 2002: 205. ISBN 1-930832-02-8.
^ Edoardo Sernesi, J. Montaldi. Linear Algebra: A Geometric Approach. CRC Press. 1993: 95. ISBN 0-412-40680-2.
^
J X Zheng-Johansson and Per-Ivar Johansson. Unification of Classical, Quantum and Relativistic Mechanics and of the Four Forces. Nova Publishers. 2006: 13. ISBN 1-59454-260-0.
^ William Barker & Roger Howe. Continuous symmetry: from Euclid to Klein. American Mathematical Society. 2008: 18 ff. ISBN 0-8218-3900-4.
^ Arlan Ramsay & Robert D. Richtmyer. Introduction to Hyperbolic Geometry. Springer. 1995: 11. ISBN 0-387-94339-0.
^ According to Hawking and Ellis: "A manifold is a space locally similar to Euclidean space in that it can be covered by coordinate patches. This structure allows differentiation to be defined, but does not distinguish between different coordinate systems. Thus, the only concepts defined by the manifold structure are those that are independent of the choice of a coordinate system." Stephen W. Hawking & George Francis Rayner Ellis. The Large Scale Structure of Space-Time. Cambridge University Press. 1973: 11. ISBN 0-521-09906-4. A mathematical definition is: A connected Hausdorff space M is called an n-dimensional manifold if each point of M is contained in an open set that is homeomorphic to an open set in Euclidean n-dimensional space.
^ Shigeyuki Morita, Teruko Nagase, Katsumi Nomizu. Geometry of Differential Forms. American Mathematical Society Bookstore. 2001: 12. ISBN 0-8218-1045-6.
^ Granino Arthur Korn, Theresa M. Korn. Mathematical handbook for scientists and engineers : definitions, theorems, and formulas for reference and review. Courier Dover Publications. 2000: 169. ISBN 0-486-41147-8.
^ 見Encarta上的定義。存檔 2009-10-31.
^ Katsu Yamane. Simulating and Generating Motions of Human Figures. Springer. 2004: 12–13. ISBN 3-540-20317-6.
^ Achilleus Papapetrou. Lectures on General Relativity. Springer. 1974: 5. ISBN 90-277-0540-2.
^ Wilford Zdunkowski & Andreas Bott. Dynamics of the Atmosphere. Cambridge University Press. 2003: 84. ISBN 0-521-00666-X.
^ A. I. Borisenko, I. E. Tarapov, Richard A. Silverman. Vector and Tensor Analysis with Applications. Courier Dover Publications. 1979: 86. ISBN 0-486-63833-2.
^ See Arvind Kumar & Shrish Barve. How and Why in Basic Mechanics. Orient Longman. 2003: 115. ISBN 81-7371-420-7.
^ Chris Doran & Anthony Lasenby. Geometric Algebra for Physicists. Cambridge University Press. 2003: §5.2.2, p. 133. ISBN 978-0-521-71595-9. .
^ For example, Møller states: "Instead of Cartesian coordinates we can obviously just as well employ general curvilinear coordinates for the fixation of points in physical space.…we shall now introduce general "curvilinear" coordinates xi in four-space…." C. Møller. The Theory of Relativity. Oxford University Press. 1952: 222 and p. 233.
^ A. P. Lightman, W. H. Press, R. H. Price & S. A. Teukolsky. Problem Book in Relativity and Gravitation. Princeton University Press. 1975: 15. ISBN 0-691-08162-X.
^ Richard L Faber. Differential Geometry and Relativity Theory: an introduction. CRC Press. 1983: 211. ISBN 0-8247-1749-X.
^ Richard Wolfson. Simply Einstein. W W Norton & Co. 2003: 216. ISBN 0-393-05154-4.
^ See Guido Rizzi, Matteo Luca Ruggiero. Relativity in rotating frames. Springer. 2003: 33. ISBN 1-4020-1805-3. .
外部連結
Cultural Frame of Reference[永久失效連結]
- Philosophical Frame of Reference
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![{mathbf {r}}=[x^{1}, x^{2}, dots ,x^{n}] .](https://wikimedia.org/api/rest_v1/media/math/render/svg/d77ca41fbd7ae5a9deac0187b55635d1afae0092)
























