Jtdcftul

图示遵守开普勒行星运动定律的两个行星轨道。 （1）行星轨道是椭圆軌道。第一个行星的轨道焦点是f1与f2，第二个行星的轨道焦点是f1与f3。太阳的位置是在点f1。 （2）A1与A2是两个面积相等的阴影区域。太陽与第一个行星的連線，扫过这两个阴影区域，所需的時間相等。（3）各个行星绕太阳公转周期的比率为a1^3/2:a2^3/2 ；这里，a1与a2分别为第一个行星与第二个行星的半长轴长度。

开普勒定律是开普勒所发现、关于行星运动的定律。他於1609年在他出版的《新天文学》科學雜誌上发表了关于行星运动的两条定律，又於1618年，发现了第三条定律。

开普勒幸运地得到了著名丹麦天文学家第谷·布拉赫所观察与收集、且非常精确的天文資料。大约于1605年，根据布拉赫的行星位置資料，开普勒发现行星的移动遵守著三条相当简单的定律。同年年底，他撰寫完成了發表文稿。但是，直到1609年，才在《新天文学》科學雜誌發表，這是因為布拉赫的觀察數據屬於他的繼承人，不能隨便讓別人使用，因此產生的一些法律糾紛造成了延遲。

在天文学与物理学上、开普勒的定律给予亚里士多德派与托勒密派极大的挑战。他主张地球是不斷地移动的；行星轨道不是圓形（epicycle）的，而是椭圆形的；行星公转的速度不等恒。这些论点，大大地动摇了当时的天文学与物理学。经过了几乎一個世纪披星戴月，废寝忘食的研究，物理学家终于能够運用物理理论解释其中的奧秘。艾萨克·牛顿應用他的第二定律和万有引力定律，在数学上严格地証明了开普勒定律，也让人们了解了其中的物理意义。

开普勒定律

开普勒的三条行星运动定律改变了整个天文学，彻底摧毁了托勒密复杂的宇宙体系，完善并简化了哥白尼的日心说。

开普勒第一定律

根據开普勒第一定律，太陽位於橢圓軌道的一個焦點。

开普勒第一定律，也称為椭圆定律、軌道定律：每一个行星都沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点中。^[1]

开普勒第二定律

根據开普勒第二定律，在同樣時間間隔內，行星繞著太陽公轉所掃過的面積相等。

开普勒第二定律，也称為等面积定律：在相等时间内，太阳和运动着的行星的连线所扫过的面积都是相等的。^[1]

这一定律实际揭示了行星绕太阳公转的角动量守恒。用公式表示为

SAB=SCD=SEK{displaystyle S_{AB}=S_{CD}=S_{EK}} 。

开普勒第三定律

根據开普勒第三定律，行星繞著太陽公轉的周期平方和它们的椭圆轨道的半长轴立方成正比。

开普勒第三定律，也稱為週期定律：各个行星绕太阳公转周期的平方和它们的椭圆轨道的半长轴的立方成正比。^[1]

由这一定律不难导出：行星与太阳之间的引力与半径的平方成反比。这是艾萨克·牛顿的万有引力定律的一个重要基础。

用公式表示为

τ2a3=K{displaystyle {frac {tau ^{2}}{a^{3}}}=K} ；

这里，a{displaystyle a} 是行星公转轨道半长轴，τ{displaystyle tau } 是行星公转周期，K{displaystyle K} 是常数。

数学推导：由牛顿万有引力定律导出开普勒定律

开普勒定律描述的是行星围绕太阳的运动，牛顿定律可以更广义地描述几个粒子因万有引力相互吸引而形成的运动。假設只有两个粒子，其中一个粒子超轻于另外一个粒子，則轻的粒子会绕著重的粒子運动，就好似行星根据开普勒定律绕著太阳運动。另外，牛顿定律还可計算出關於其它方面的解答，行星轨道可以呈抛物线运动或双曲线运动。这是开普勒定律所无法预测到的結果。在一个粒子并不超轻于另外一个粒子的状况下，依照广义二体问题的解答，每一个粒子會绕著它们的共同质心運动。这也是开普勒定律无法预测到的。

开普勒定律使用几何语言将行星的坐标及时间跟轨道参数相连结。牛顿第二定律是一个微分方程式。开普勒定律的推导涉及一些解析微分方程式的技巧。在推導开普勒第一定律之前，必須先推导出开普勒第二定律，因为开普勒第一定律需要用到开普勒第二定律裏的一些計算結果。

开普勒第二定律推导

牛顿万有引力定律表明，任意两个粒子由通过连线方向的力相互吸引。该引力的的大小与它们的质量乘积成正比，与它们距离的平方成反比。由于太阳超重于行星，可以假设太阳是固定的。用方程式表示，

F=−GmMr2 r^{displaystyle {boldsymbol {F}}=-G{frac {mM}{r^{2}}} {hat {boldsymbol {r}}}} ；

这裏，F{displaystyle {boldsymbol {F}}} 是太阳作用於行星的万有引力，m{displaystyle m} 是行星的质量，M{displaystyle M} 是太阳的质量，r{displaystyle {boldsymbol {r}}} 是行星相对于太阳的位移向量，r^{displaystyle {hat {boldsymbol {r}}}} 是 r{displaystyle {boldsymbol {r}}} 的单位向量。

牛顿第二定律表明，物體受力後所产生的加速度 r¨{displaystyle {ddot {boldsymbol {r}}}} ，和其所受的淨力 F{displaystyle {boldsymbol {F}}} 成正比，和其質量 m{displaystyle m} 成反比，以方程式表示，

F=mr¨{displaystyle {boldsymbol {F}}=m{ddot {boldsymbol {r}}}} 。

合并这两个方程式，

r¨=−GMr2 r^{displaystyle {ddot {boldsymbol {r}}}=-G{frac {M}{r^{2}}} {hat {boldsymbol {r}}}} 。 (1)

思考位置向量 r=rr^{displaystyle {boldsymbol {r}}=r{hat {boldsymbol {r}}}} ，對於时间 t{displaystyle t} 微分一次可得到速度向量，再微分一次则可得到加速度向量：

r˙=r˙r^+rθ˙θ^{displaystyle {dot {boldsymbol {r}}}={dot {r}}{hat {boldsymbol {r}}}+r{dot {theta }}{hat {boldsymbol {theta }}}} ，

r¨=(r¨r^+r˙dr^dt)+(r˙θ˙θ^+rθ¨θ^+rθ˙dθ^dt)=(r¨−rθ˙2)r^+(rθ¨+2r˙θ˙)θ^{displaystyle {ddot {boldsymbol {r}}}=left({ddot {r}}{hat {boldsymbol {r}}}+{dot {r}}{frac {mathrm {d} {hat {boldsymbol {r}}}}{mathrm {d} t}}right)+left({dot {r}}{dot {theta }}{hat {boldsymbol {theta }}}+r{ddot {theta }}{hat {boldsymbol {theta }}}+r{dot {theta }}{frac {mathrm {d} {hat {boldsymbol {theta }}}}{mathrm {d} t}}right)=({ddot {r}}-r{dot {theta }}^{2}){hat {boldsymbol {r}}}+(r{ddot {theta }}+2{dot {r}}{dot {theta }}){hat {boldsymbol {theta }}}} 。(2)

在这里，用到了单位向量微分方程式：

dr^dt=θ˙θ^{displaystyle {frac {mathrm {d} {hat {boldsymbol {r}}}}{mathrm {d} t}}={dot {theta }}{hat {boldsymbol {theta }}}} ，

dθ^dt=−θ˙r^{displaystyle {frac {mathrm {d} {hat {boldsymbol {theta }}}}{mathrm {d} t}}=-{dot {theta }}{hat {boldsymbol {r}}}} 。

合并方程式 (1) 与 (2) ，可以得到向量运动方程式：

(r¨−rθ˙2)r^+(rθ¨+2r˙θ˙)θ^=−GMr2r^{displaystyle ({ddot {r}}-r{dot {theta }}^{2}){hat {boldsymbol {r}}}+(r{ddot {theta }}+2{dot {r}}{dot {theta }}){hat {boldsymbol {theta }}}=-{frac {GM}{r^{2}}}{hat {boldsymbol {r}}}}

取各个分量，可以得到两个常微分方程式，一个是关于径向加速度，另一个是关于切向加速度：

r¨−rθ˙2=−GMr2{displaystyle {ddot {r}}-r{dot {theta }}^{2}=-{frac {GM}{r^{2}}}} ，(3)

rθ¨+2r˙θ˙=0{displaystyle r{ddot {theta }}+2{dot {r}}{dot {theta }}=0} 。(4)

导引开普勒第二定律只需切向加速度方程式。试想行星的角动量 ℓ=mr2θ˙{displaystyle ell =mr^{2}{dot {theta }}} 。由于行星的质量是常数，角动量對於时间的导数为

ℓ˙=mr(2r˙θ˙+rθ¨)=0{displaystyle {dot {ell }}=mr(2{dot {r}}{dot {theta }}+r{ddot {theta }})=0} 。

角动量 ℓ{displaystyle ell } 也是一个运动常数，即使距离 r{displaystyle r} 与角速度 θ˙{displaystyle {dot {theta }}} 都可能会随时间变化。

从时间 t1{displaystyle t_{1}} 到时间 t2{displaystyle t_{2}} 扫过的区域 ΔA{displaystyle Delta A} ，

ΔA=∫t1t212⋅r⋅rθ˙⋅dt=∫t1t2ℓ2mdt=ℓ2m⋅(t2−t1){displaystyle Delta A=int _{t_{1}}^{t_{2}}{frac {1}{2}}cdot rcdot r{dot {theta }}cdot mathrm {d} t=int _{t_{1}}^{t_{2}}{frac {ell }{2m}}mathrm {d} t={frac {ell }{2m}}cdot (t_{2}-t_{1})} 。

行星太阳连线扫过的区域面积相依于间隔时间 t2−t1{displaystyle t_{2}-t_{1}} 。所以，开普勒第二定律是正确的。

开普勒第一定律推导

设定 u=1r{displaystyle u={frac {1}{r}}} 。这样，角速度是

θ˙=ℓmr2=ℓu2m{displaystyle {dot {theta }}={frac {ell }{mr^{2}}}={frac {ell u^{2}}{m}}} 。

对时间微分和对角度微分有如下关系：

ddt=θ˙ddθ=ℓu2mddθ{displaystyle {frac {mathrm {d} }{mathrm {d} t}}={dot {theta }}{frac {mathrm {d} }{mathrm {d} theta }}={frac {ell u^{2}}{m}}{frac {mathrm {d} }{mathrm {d} theta }}} 。

根据上述关系，径向距离 r=1u{displaystyle r={frac {1}{u}}} 对时间的导数为：

r˙=ℓu2mddθ1u=−ℓu2m1u2dudθ=−ℓmdudθ{displaystyle {dot {r}}={frac {ell u^{2}}{m}}{frac {mathrm {d} }{mathrm {d} theta }}{frac {1}{u}}=-{frac {ell u^{2}}{m}}{frac {1}{u^{2}}}{frac {mathrm {d} u}{mathrm {d} theta }}=-{frac {ell }{m}}{frac {mathrm {d} u}{mathrm {d} theta }}} 。

再求一次导数：

r¨=ℓu2mdr˙dθ=ℓu2mddθ(−ℓmdudθ)=−ℓ2u2m2d2udθ2{displaystyle {ddot {r}}={frac {ell u^{2}}{m}}{frac {mathrm {d} {dot {r}}}{mathrm {d} theta }}={frac {ell u^{2}}{m}}{frac {mathrm {d} }{mathrm {d} theta }}(-{frac {ell }{m}}{frac {mathrm {d} u}{mathrm {d} theta }})=-{frac {ell ^{2}u^{2}}{m^{2}}}{frac {mathrm {d} ^{2}u}{mathrm {d} theta ^{2}}}} 。

代入径向运动方程式 (3) ，r¨−rθ˙2=−GMr2{displaystyle {ddot {r}}-r{dot {theta }}^{2}=-{frac {GM}{r^{2}}}} ，

−ℓ2u2m2d2udθ2−ℓ2u3m2=−GMu2{displaystyle -{frac {ell ^{2}u^{2}}{m^{2}}}{frac {mathrm {d} ^{2}u}{mathrm {d} theta ^{2}}}-{frac {ell ^{2}u^{3}}{m^{2}}}=-GMu^{2}} 。

将此方程式除以 −ℓ2u2m2{displaystyle -{frac {ell ^{2}u^{2}}{m^{2}}}} ，则可得到一个简单的常係数非齐次线性全微分方程式来描述行星轨道：

d2udθ2+u=GMm2ℓ2{displaystyle {frac {mathrm {d} ^{2}u}{mathrm {d} theta ^{2}}}+u={frac {GMm^{2}}{ell ^{2}}}} 。

为了解这个微分方程，先列出一个特解

u=GMm2ℓ2{displaystyle u={frac {GMm^{2}}{ell ^{2}}}} 。

再求解剩余的常系数齐次线性全微分方程式，

d2udθ2+u=0{displaystyle {frac {mathrm {d} ^{2}u}{mathrm {d} theta ^{2}}}+u=0} 。

它的解为

u=C cos⁡(θ−θ0){displaystyle u=C cos(theta -theta _{0})} ；

这里，C{displaystyle C} 与 θ0{displaystyle theta _{0}} 是常数。合并特解和与齐次方程解，可以得到通解

u=GMm2ℓ2+C cos⁡(θ−θ0){displaystyle u={frac {GMm^{2}}{ell ^{2}}}+C cos(theta -theta _{0})} 。

选择坐标轴，让 θ0=0{displaystyle theta _{0}=0} 。代回 u=1r{displaystyle u={frac {1}{r}}} ，

1r=GMm2ℓ2(1+e cos⁡θ){displaystyle {frac {1}{r}}={frac {GMm^{2}}{ell ^{2}}}(1+e cos {theta })} ；

其中，e=Cℓ2/GMm2{displaystyle e=Cell ^{2}/GMm^{2}} 是离心率。

这是圆锥曲线的极坐标方程式，坐标系的原点是圆锥曲线的焦点之一。假若 0<e<1{displaystyle 0<e<1} ，则 r{displaystyle r} 所描述的是椭圆轨道。這证明了开普勒第一定律。

开普勒第三定律推导

在建立牛顿万有引力定律的概念与数学架构上，开普勒第三定律是牛顿依据的重要线索之一。假若接受牛顿运动定律。试想一个虚拟行星环绕着太阳公转，行星的移动轨道恰巧呈圆形，轨道半径为 r{displaystyle r} 。那么，太阳作用于行星的万有引力为 F=mv2r{displaystyle F={frac {mv^{2}}{r}}} 。行星移动速度为 v=2πrτ{displaystyle v={frac {2pi r}{tau }}} 。依照开普勒第三定律，这速度 v{displaystyle v} 与半径的平方根 r{displaystyle {sqrt {r}}} 成反比。所以，万有引力 F∝1r2{displaystyle Fpropto {frac {1}{r^{2}}}} 。猜想这大概是牛顿发现万有引力定律的思路，但这个猜想无法被证实，因为在他的计算本里，并沒有找到任何关于这方面的证据。

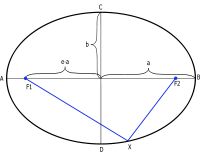
行星环绕太阳（焦点 F1 ）的椭圆轨道。

开普勒第一定律阐明，行星环绕太阳的轨道是椭圆形的。椭圆的面积是 πab{displaystyle pi ab} ；这里，a{displaystyle a} 与 b{displaystyle b} 分别为椭圆的半长轴与半短轴。在开普勒第二定律推导里，行星－太阳连线扫过区域速度 dAdt{displaystyle {frac {mathrm {d} A}{mathrm {d} t}}} 为

dAdt=ℓ2m{displaystyle {frac {mathrm {d} A}{mathrm {d} t}}={frac {ell }{2m}}} 。

所以，行星公转周期 τ{displaystyle tau } 为

τ=2mπabℓ{displaystyle tau ={frac {2mpi ab}{ell }}} 。(5)

关于此行星环绕太阳，椭圆的半長軸 a{displaystyle a} ，半短軸 b{displaystyle b} 与近拱距 rA{displaystyle r_{A}} （近拱点 A 与引力中心之间的距离），远拱距 rB{displaystyle r_{B}} （远拱点 B 与引力中心之间的距离）的关系分别为

a=rA+rB2{displaystyle a={frac {r_{A}+r_{B}}{2}}} ，(6)

b=rA rB{displaystyle b={sqrt {r_{A} r_{B}}}} 。(7)

如果想要知道半長軸与半短軸，必须先求得近拱距与远拱距。依据能量守恒定律，

E=12mr˙2+12mr2θ˙2−GmMr{displaystyle E={frac {1}{2}}m{dot {r}}^{2}+{frac {1}{2}}mr^{2}{dot {theta }}^{2}-G{frac {mM}{r}}} 。

在近拱点 A 与远拱点 B，径向速度都等于零：

r˙=0{displaystyle {dot {r}}=0} 。

所以，

E=12mr2θ˙2−GmMr=ℓ22mr2−GmMr{displaystyle E={frac {1}{2}}mr^{2}{dot {theta }}^{2}-G{frac {mM}{r}}={frac {ell ^{2}}{2mr^{2}}}-G{frac {mM}{r}}} 。

稍为加以编排，可以得到 r{displaystyle r} 的一元二次方程式：

r2+GmMEr−ℓ22mE=0{displaystyle r^{2}+{frac {GmM}{E}}r-{frac {ell ^{2}}{2mE}}=0} 。

其兩個根分别为椭圆轨道的近拱距 rA{displaystyle r_{A}} 与远拱距 rB{displaystyle r_{B}} 。

rA=−GmME−(GmME)2+2ℓ2mE2{displaystyle r_{A}=-{frac {{frac {GmM}{E}}-{sqrt {left({frac {GmM}{E}}right)^{2}+{frac {2ell ^{2}}{mE}}}}}{2}}} ；

rB=−GmME+(GmME)2+2ℓ2mE2{displaystyle r_{B}=-{frac {{frac {GmM}{E}}+{sqrt {left({frac {GmM}{E}}right)^{2}+{frac {2ell ^{2}}{mE}}}}}{2}}} 。

代入方程式 (6) 与 (7) ，

a=−GmM2E{displaystyle a=-{frac {GmM}{2E}}} ，

b=ℓ−2mE=ℓmaGM{displaystyle b={frac {ell }{sqrt {-2mE}}}={frac {ell }{m}}{frac {sqrt {a}}{sqrt {GM}}}} 。

代入方程式 (5) ，周期的方程式为

τ=2πa3/2GM{displaystyle tau ={frac {2pi a^{3/2}}{sqrt {GM}}}} 。

■

參見

• 开普勒


• 牛顿第二定律


• 万有引力定律


• 《新天文學》


• 《世界的和諧》


• 牛頓旋轉軌道定理

參考資料

1. 
   ^ ^1.01.11.2 克卜勒的行星運動三定律 (PDF). 高苑科技大學. [2015-07-26].