Eigenvalue estimates for operator perturbations
$begingroup$
I edited the question to a general mathematical question, since I found the answer in Carlo Beenakker's reference and think that my initial question was mathematically misleading.
What was behind all this was: If we take $W_N$ being trace free skew-symmetric matrices of rank $N$ on an $N$-dimensional space. And we perturb each of them with a positive operator $A_N$ such that all of the $A_N$ have the same trace. Is it true that as $N rightarrow infty$ the real part of some eigenvalue will tend to zero (resp. be zero)?
Answer:
The answer is yes by the following identity $$operatorname{tr}(A_N)=operatorname{Re}operatorname{tr}(W_N+A_N) = sum_{lambda in sigma(W_N+A_N)} operatorname{Re}(lambda).$$
Since the left-hand side is finite, the right-hand side has to converge.
fa.functional-analysis real-analysis ap.analysis-of-pdes ca.classical-analysis-and-odes sp.spectral-theory
$endgroup$
add a comment |
$begingroup$
I edited the question to a general mathematical question, since I found the answer in Carlo Beenakker's reference and think that my initial question was mathematically misleading.
What was behind all this was: If we take $W_N$ being trace free skew-symmetric matrices of rank $N$ on an $N$-dimensional space. And we perturb each of them with a positive operator $A_N$ such that all of the $A_N$ have the same trace. Is it true that as $N rightarrow infty$ the real part of some eigenvalue will tend to zero (resp. be zero)?
Answer:
The answer is yes by the following identity $$operatorname{tr}(A_N)=operatorname{Re}operatorname{tr}(W_N+A_N) = sum_{lambda in sigma(W_N+A_N)} operatorname{Re}(lambda).$$
Since the left-hand side is finite, the right-hand side has to converge.
fa.functional-analysis real-analysis ap.analysis-of-pdes ca.classical-analysis-and-odes sp.spectral-theory
$endgroup$
$begingroup$
What is your definition of "dissipative system"? If it's simply that the spectrum has negative real part I don't see why that should be true. There are purely dissipative systems for which the spectrum is and stays entirely real
$endgroup$
– lcv
7 hours ago
$begingroup$
yes, that's true and yes that's my definition. However, in this particular case, there is a special dynamics that is mixing (the Laplacian connects all components of the system). Therefore, it is believable that it holds in this case. Please have a look at Carlo Beenakker's answer below and also the comments.
$endgroup$
– Sascha
7 hours ago
$begingroup$
See Carlo Beenakker's comment about $delta N/ N$ being finite. But this is an additional assumption. I.e. if you perturb a skewhermitian with a negative operator you may (or not) end up with some imaginary eigenvalues if the perturbation is suitably small or vanishing.
$endgroup$
– lcv
7 hours ago
$begingroup$
Sorry, I don't understand. $delta N=1$ in my case. So $delta N/N$ goes to zero. So according to him some eigenvalues should approach the imaginary axis and that is what I would like to show. I agree that this might not hold for general perturbations of skew-symmetric matrices, but the system I consider is somewhat special.-But I feel I have not understood your commet fully.
$endgroup$
– Sascha
6 hours ago
add a comment |
$begingroup$
I edited the question to a general mathematical question, since I found the answer in Carlo Beenakker's reference and think that my initial question was mathematically misleading.
What was behind all this was: If we take $W_N$ being trace free skew-symmetric matrices of rank $N$ on an $N$-dimensional space. And we perturb each of them with a positive operator $A_N$ such that all of the $A_N$ have the same trace. Is it true that as $N rightarrow infty$ the real part of some eigenvalue will tend to zero (resp. be zero)?
Answer:
The answer is yes by the following identity $$operatorname{tr}(A_N)=operatorname{Re}operatorname{tr}(W_N+A_N) = sum_{lambda in sigma(W_N+A_N)} operatorname{Re}(lambda).$$
Since the left-hand side is finite, the right-hand side has to converge.
fa.functional-analysis real-analysis ap.analysis-of-pdes ca.classical-analysis-and-odes sp.spectral-theory
$endgroup$
I edited the question to a general mathematical question, since I found the answer in Carlo Beenakker's reference and think that my initial question was mathematically misleading.
What was behind all this was: If we take $W_N$ being trace free skew-symmetric matrices of rank $N$ on an $N$-dimensional space. And we perturb each of them with a positive operator $A_N$ such that all of the $A_N$ have the same trace. Is it true that as $N rightarrow infty$ the real part of some eigenvalue will tend to zero (resp. be zero)?
Answer:
The answer is yes by the following identity $$operatorname{tr}(A_N)=operatorname{Re}operatorname{tr}(W_N+A_N) = sum_{lambda in sigma(W_N+A_N)} operatorname{Re}(lambda).$$
Since the left-hand side is finite, the right-hand side has to converge.
fa.functional-analysis real-analysis ap.analysis-of-pdes ca.classical-analysis-and-odes sp.spectral-theory
fa.functional-analysis real-analysis ap.analysis-of-pdes ca.classical-analysis-and-odes sp.spectral-theory
edited 2 hours ago
Sascha
asked 8 hours ago
SaschaSascha
447114
447114
$begingroup$
What is your definition of "dissipative system"? If it's simply that the spectrum has negative real part I don't see why that should be true. There are purely dissipative systems for which the spectrum is and stays entirely real
$endgroup$
– lcv
7 hours ago
$begingroup$
yes, that's true and yes that's my definition. However, in this particular case, there is a special dynamics that is mixing (the Laplacian connects all components of the system). Therefore, it is believable that it holds in this case. Please have a look at Carlo Beenakker's answer below and also the comments.
$endgroup$
– Sascha
7 hours ago
$begingroup$
See Carlo Beenakker's comment about $delta N/ N$ being finite. But this is an additional assumption. I.e. if you perturb a skewhermitian with a negative operator you may (or not) end up with some imaginary eigenvalues if the perturbation is suitably small or vanishing.
$endgroup$
– lcv
7 hours ago
$begingroup$
Sorry, I don't understand. $delta N=1$ in my case. So $delta N/N$ goes to zero. So according to him some eigenvalues should approach the imaginary axis and that is what I would like to show. I agree that this might not hold for general perturbations of skew-symmetric matrices, but the system I consider is somewhat special.-But I feel I have not understood your commet fully.
$endgroup$
– Sascha
6 hours ago
add a comment |
$begingroup$
What is your definition of "dissipative system"? If it's simply that the spectrum has negative real part I don't see why that should be true. There are purely dissipative systems for which the spectrum is and stays entirely real
$endgroup$
– lcv
7 hours ago
$begingroup$
yes, that's true and yes that's my definition. However, in this particular case, there is a special dynamics that is mixing (the Laplacian connects all components of the system). Therefore, it is believable that it holds in this case. Please have a look at Carlo Beenakker's answer below and also the comments.
$endgroup$
– Sascha
7 hours ago
$begingroup$
See Carlo Beenakker's comment about $delta N/ N$ being finite. But this is an additional assumption. I.e. if you perturb a skewhermitian with a negative operator you may (or not) end up with some imaginary eigenvalues if the perturbation is suitably small or vanishing.
$endgroup$
– lcv
7 hours ago
$begingroup$
Sorry, I don't understand. $delta N=1$ in my case. So $delta N/N$ goes to zero. So according to him some eigenvalues should approach the imaginary axis and that is what I would like to show. I agree that this might not hold for general perturbations of skew-symmetric matrices, but the system I consider is somewhat special.-But I feel I have not understood your commet fully.
$endgroup$
– Sascha
6 hours ago
$begingroup$
What is your definition of "dissipative system"? If it's simply that the spectrum has negative real part I don't see why that should be true. There are purely dissipative systems for which the spectrum is and stays entirely real
$endgroup$
– lcv
7 hours ago
$begingroup$
What is your definition of "dissipative system"? If it's simply that the spectrum has negative real part I don't see why that should be true. There are purely dissipative systems for which the spectrum is and stays entirely real
$endgroup$
– lcv
7 hours ago
$begingroup$
yes, that's true and yes that's my definition. However, in this particular case, there is a special dynamics that is mixing (the Laplacian connects all components of the system). Therefore, it is believable that it holds in this case. Please have a look at Carlo Beenakker's answer below and also the comments.
$endgroup$
– Sascha
7 hours ago
$begingroup$
yes, that's true and yes that's my definition. However, in this particular case, there is a special dynamics that is mixing (the Laplacian connects all components of the system). Therefore, it is believable that it holds in this case. Please have a look at Carlo Beenakker's answer below and also the comments.
$endgroup$
– Sascha
7 hours ago
$begingroup$
See Carlo Beenakker's comment about $delta N/ N$ being finite. But this is an additional assumption. I.e. if you perturb a skewhermitian with a negative operator you may (or not) end up with some imaginary eigenvalues if the perturbation is suitably small or vanishing.
$endgroup$
– lcv
7 hours ago
$begingroup$
See Carlo Beenakker's comment about $delta N/ N$ being finite. But this is an additional assumption. I.e. if you perturb a skewhermitian with a negative operator you may (or not) end up with some imaginary eigenvalues if the perturbation is suitably small or vanishing.
$endgroup$
– lcv
7 hours ago
$begingroup$
Sorry, I don't understand. $delta N=1$ in my case. So $delta N/N$ goes to zero. So according to him some eigenvalues should approach the imaginary axis and that is what I would like to show. I agree that this might not hold for general perturbations of skew-symmetric matrices, but the system I consider is somewhat special.-But I feel I have not understood your commet fully.
$endgroup$
– Sascha
6 hours ago
$begingroup$
Sorry, I don't understand. $delta N=1$ in my case. So $delta N/N$ goes to zero. So according to him some eigenvalues should approach the imaginary axis and that is what I would like to show. I agree that this might not hold for general perturbations of skew-symmetric matrices, but the system I consider is somewhat special.-But I feel I have not understood your commet fully.
$endgroup$
– Sascha
6 hours ago
add a comment |
1 Answer
1
active
oldest
votes
$begingroup$
This problem of "non-Hermitian" quantum mechanics has been studied in the context of random-matrix theory (RMT), see for example the review Random matrix approaches to open quantum systems. The particular case pointed to in the OP is when the Hermitian matrix ${cal H}=iW_{H}$ of high rank $N$ is perturbed by a positive-definite matrix $-ipi WW^{t}$ of low rank $delta Nll N$. The eigenvalues $E_n-iGamma_n$ of the effective Hamiltonian ${cal H}_{text{eff}}={cal H}-ipi WW^t$ describe resonant scattering from a heavy atom or quantum dot (with $E_n$ the center of the resonance and $Gamma_n$ its width). The special case in the OP where ${cal H}$ is block-off-diagonal is referred to as the case of "chiral symmetry" in the context of random-matrix theory. (The appropriate ensemble for real ${cal H}$ is the socalled "chiral orthogonal ensemble".)
Now the question in the OP is the distribution of the $Gamma_n$'s in the limit $Nrightarrowinfty$ at fixed $delta N$. The "universal" result of random-matrix theory (see section IV.A in the cited review) is that for $delta Nll N$ all $Gamma_n$'s are greater than a minimal value $Gamma_{text{min}}simeqdelta N/N$ and they accumulate near that value.
Note that the OP refers to $i$ times the eigenvalues of ${cal H}$, so this approach to the real axis corresponds to an approach to the imaginary axis in the OP.
Hence my answer to the final question of the OP, "does the spectrum approach the imaginary axis in the large-$N$ limit" is yes, it does, if the non-Hermitian perturbation has a rank $delta N$ that remains small compared to the rank of the Hermitian part. There remains, however, for any finite $N$ a gap of order $delta N/N$ that separates the "dissipative dynamics" from the unitary quantum mechanical evolution.
I show a plot that illustrates the clustering of the eigenvalues $E_n-iGamma_n$ of ${cal H}_{text{eff}}$ near the $Gamma=0$ axis, with a sharp threshold (blue horizontal line) and a gap.
In the plot $N=500$ and $delta N=50$. There is no chiral symmetry, but that would only introduce a $pm E_n$ symmetry, it would not affect the gap in the $Gamma$'s.
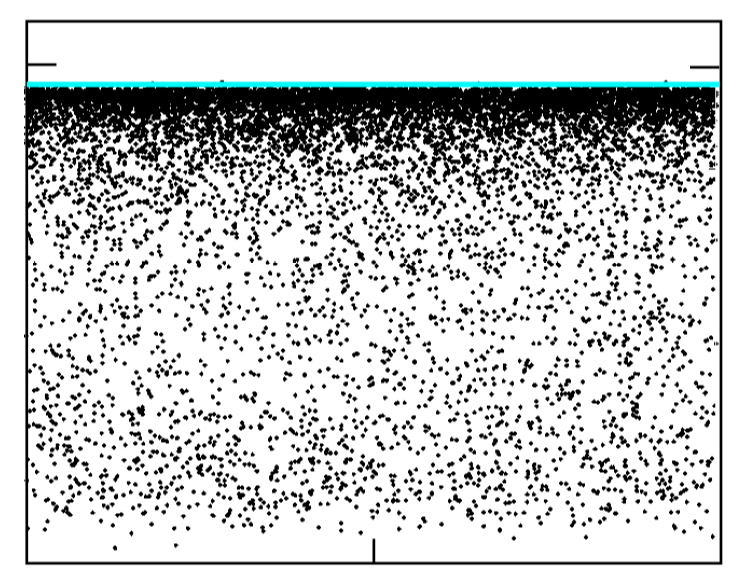
source: arXiv:1405.6896
$endgroup$
$begingroup$
First, I would like to thank you for your deep insights into my question. It gives I think a lot of intuition about why this should hold. Can I however still ask you though whether the result you are referring to is rigorous?-PS: I really think what you write is very interesting for me.
$endgroup$
– Sascha
7 hours ago
1
$begingroup$
it is rigorous in the context of random-matrix theory, so for the gaussian ensembles; like all the RMT results, it is believed to hold for a much wider class of random matrices.
$endgroup$
– Carlo Beenakker
7 hours ago
$begingroup$
ah, but so it is not necessarily clear for my deterministic sequence above, right?
$endgroup$
– Sascha
7 hours ago
1
$begingroup$
not necessarily so, but keep in mind that RMT was developed for deterministic systems, such as large molecules. The randomness is introduced to make the problem tractable, RMT is believed to hold for deterministic systems if they are sufficiently complex ("chaotic dynamics" is the term). It has really a remarkably wide range of applicability, it is in fact the other way around: you have to work really hard to see behavior that deviates from the universal RMT results.
$endgroup$
– Carlo Beenakker
7 hours ago
add a comment |
Your Answer
StackExchange.ifUsing("editor", function () {
return StackExchange.using("mathjaxEditing", function () {
StackExchange.MarkdownEditor.creationCallbacks.add(function (editor, postfix) {
StackExchange.mathjaxEditing.prepareWmdForMathJax(editor, postfix, [["$", "$"], ["\\(","\\)"]]);
});
});
}, "mathjax-editing");
StackExchange.ready(function() {
var channelOptions = {
tags: "".split(" "),
id: "504"
};
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function() {
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled) {
StackExchange.using("snippets", function() {
createEditor();
});
}
else {
createEditor();
}
});
function createEditor() {
StackExchange.prepareEditor({
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: true,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: 10,
bindNavPrevention: true,
postfix: "",
imageUploader: {
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
},
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
});
}
});
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmathoverflow.net%2fquestions%2f323957%2feigenvalue-estimates-for-operator-perturbations%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
1 Answer
1
active
oldest
votes
1 Answer
1
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
This problem of "non-Hermitian" quantum mechanics has been studied in the context of random-matrix theory (RMT), see for example the review Random matrix approaches to open quantum systems. The particular case pointed to in the OP is when the Hermitian matrix ${cal H}=iW_{H}$ of high rank $N$ is perturbed by a positive-definite matrix $-ipi WW^{t}$ of low rank $delta Nll N$. The eigenvalues $E_n-iGamma_n$ of the effective Hamiltonian ${cal H}_{text{eff}}={cal H}-ipi WW^t$ describe resonant scattering from a heavy atom or quantum dot (with $E_n$ the center of the resonance and $Gamma_n$ its width). The special case in the OP where ${cal H}$ is block-off-diagonal is referred to as the case of "chiral symmetry" in the context of random-matrix theory. (The appropriate ensemble for real ${cal H}$ is the socalled "chiral orthogonal ensemble".)
Now the question in the OP is the distribution of the $Gamma_n$'s in the limit $Nrightarrowinfty$ at fixed $delta N$. The "universal" result of random-matrix theory (see section IV.A in the cited review) is that for $delta Nll N$ all $Gamma_n$'s are greater than a minimal value $Gamma_{text{min}}simeqdelta N/N$ and they accumulate near that value.
Note that the OP refers to $i$ times the eigenvalues of ${cal H}$, so this approach to the real axis corresponds to an approach to the imaginary axis in the OP.
Hence my answer to the final question of the OP, "does the spectrum approach the imaginary axis in the large-$N$ limit" is yes, it does, if the non-Hermitian perturbation has a rank $delta N$ that remains small compared to the rank of the Hermitian part. There remains, however, for any finite $N$ a gap of order $delta N/N$ that separates the "dissipative dynamics" from the unitary quantum mechanical evolution.
I show a plot that illustrates the clustering of the eigenvalues $E_n-iGamma_n$ of ${cal H}_{text{eff}}$ near the $Gamma=0$ axis, with a sharp threshold (blue horizontal line) and a gap.
In the plot $N=500$ and $delta N=50$. There is no chiral symmetry, but that would only introduce a $pm E_n$ symmetry, it would not affect the gap in the $Gamma$'s.

source: arXiv:1405.6896
$endgroup$
$begingroup$
First, I would like to thank you for your deep insights into my question. It gives I think a lot of intuition about why this should hold. Can I however still ask you though whether the result you are referring to is rigorous?-PS: I really think what you write is very interesting for me.
$endgroup$
– Sascha
7 hours ago
1
$begingroup$
it is rigorous in the context of random-matrix theory, so for the gaussian ensembles; like all the RMT results, it is believed to hold for a much wider class of random matrices.
$endgroup$
– Carlo Beenakker
7 hours ago
$begingroup$
ah, but so it is not necessarily clear for my deterministic sequence above, right?
$endgroup$
– Sascha
7 hours ago
1
$begingroup$
not necessarily so, but keep in mind that RMT was developed for deterministic systems, such as large molecules. The randomness is introduced to make the problem tractable, RMT is believed to hold for deterministic systems if they are sufficiently complex ("chaotic dynamics" is the term). It has really a remarkably wide range of applicability, it is in fact the other way around: you have to work really hard to see behavior that deviates from the universal RMT results.
$endgroup$
– Carlo Beenakker
7 hours ago
add a comment |
$begingroup$
This problem of "non-Hermitian" quantum mechanics has been studied in the context of random-matrix theory (RMT), see for example the review Random matrix approaches to open quantum systems. The particular case pointed to in the OP is when the Hermitian matrix ${cal H}=iW_{H}$ of high rank $N$ is perturbed by a positive-definite matrix $-ipi WW^{t}$ of low rank $delta Nll N$. The eigenvalues $E_n-iGamma_n$ of the effective Hamiltonian ${cal H}_{text{eff}}={cal H}-ipi WW^t$ describe resonant scattering from a heavy atom or quantum dot (with $E_n$ the center of the resonance and $Gamma_n$ its width). The special case in the OP where ${cal H}$ is block-off-diagonal is referred to as the case of "chiral symmetry" in the context of random-matrix theory. (The appropriate ensemble for real ${cal H}$ is the socalled "chiral orthogonal ensemble".)
Now the question in the OP is the distribution of the $Gamma_n$'s in the limit $Nrightarrowinfty$ at fixed $delta N$. The "universal" result of random-matrix theory (see section IV.A in the cited review) is that for $delta Nll N$ all $Gamma_n$'s are greater than a minimal value $Gamma_{text{min}}simeqdelta N/N$ and they accumulate near that value.
Note that the OP refers to $i$ times the eigenvalues of ${cal H}$, so this approach to the real axis corresponds to an approach to the imaginary axis in the OP.
Hence my answer to the final question of the OP, "does the spectrum approach the imaginary axis in the large-$N$ limit" is yes, it does, if the non-Hermitian perturbation has a rank $delta N$ that remains small compared to the rank of the Hermitian part. There remains, however, for any finite $N$ a gap of order $delta N/N$ that separates the "dissipative dynamics" from the unitary quantum mechanical evolution.
I show a plot that illustrates the clustering of the eigenvalues $E_n-iGamma_n$ of ${cal H}_{text{eff}}$ near the $Gamma=0$ axis, with a sharp threshold (blue horizontal line) and a gap.
In the plot $N=500$ and $delta N=50$. There is no chiral symmetry, but that would only introduce a $pm E_n$ symmetry, it would not affect the gap in the $Gamma$'s.

source: arXiv:1405.6896
$endgroup$
$begingroup$
First, I would like to thank you for your deep insights into my question. It gives I think a lot of intuition about why this should hold. Can I however still ask you though whether the result you are referring to is rigorous?-PS: I really think what you write is very interesting for me.
$endgroup$
– Sascha
7 hours ago
1
$begingroup$
it is rigorous in the context of random-matrix theory, so for the gaussian ensembles; like all the RMT results, it is believed to hold for a much wider class of random matrices.
$endgroup$
– Carlo Beenakker
7 hours ago
$begingroup$
ah, but so it is not necessarily clear for my deterministic sequence above, right?
$endgroup$
– Sascha
7 hours ago
1
$begingroup$
not necessarily so, but keep in mind that RMT was developed for deterministic systems, such as large molecules. The randomness is introduced to make the problem tractable, RMT is believed to hold for deterministic systems if they are sufficiently complex ("chaotic dynamics" is the term). It has really a remarkably wide range of applicability, it is in fact the other way around: you have to work really hard to see behavior that deviates from the universal RMT results.
$endgroup$
– Carlo Beenakker
7 hours ago
add a comment |
$begingroup$
This problem of "non-Hermitian" quantum mechanics has been studied in the context of random-matrix theory (RMT), see for example the review Random matrix approaches to open quantum systems. The particular case pointed to in the OP is when the Hermitian matrix ${cal H}=iW_{H}$ of high rank $N$ is perturbed by a positive-definite matrix $-ipi WW^{t}$ of low rank $delta Nll N$. The eigenvalues $E_n-iGamma_n$ of the effective Hamiltonian ${cal H}_{text{eff}}={cal H}-ipi WW^t$ describe resonant scattering from a heavy atom or quantum dot (with $E_n$ the center of the resonance and $Gamma_n$ its width). The special case in the OP where ${cal H}$ is block-off-diagonal is referred to as the case of "chiral symmetry" in the context of random-matrix theory. (The appropriate ensemble for real ${cal H}$ is the socalled "chiral orthogonal ensemble".)
Now the question in the OP is the distribution of the $Gamma_n$'s in the limit $Nrightarrowinfty$ at fixed $delta N$. The "universal" result of random-matrix theory (see section IV.A in the cited review) is that for $delta Nll N$ all $Gamma_n$'s are greater than a minimal value $Gamma_{text{min}}simeqdelta N/N$ and they accumulate near that value.
Note that the OP refers to $i$ times the eigenvalues of ${cal H}$, so this approach to the real axis corresponds to an approach to the imaginary axis in the OP.
Hence my answer to the final question of the OP, "does the spectrum approach the imaginary axis in the large-$N$ limit" is yes, it does, if the non-Hermitian perturbation has a rank $delta N$ that remains small compared to the rank of the Hermitian part. There remains, however, for any finite $N$ a gap of order $delta N/N$ that separates the "dissipative dynamics" from the unitary quantum mechanical evolution.
I show a plot that illustrates the clustering of the eigenvalues $E_n-iGamma_n$ of ${cal H}_{text{eff}}$ near the $Gamma=0$ axis, with a sharp threshold (blue horizontal line) and a gap.
In the plot $N=500$ and $delta N=50$. There is no chiral symmetry, but that would only introduce a $pm E_n$ symmetry, it would not affect the gap in the $Gamma$'s.

source: arXiv:1405.6896
$endgroup$
This problem of "non-Hermitian" quantum mechanics has been studied in the context of random-matrix theory (RMT), see for example the review Random matrix approaches to open quantum systems. The particular case pointed to in the OP is when the Hermitian matrix ${cal H}=iW_{H}$ of high rank $N$ is perturbed by a positive-definite matrix $-ipi WW^{t}$ of low rank $delta Nll N$. The eigenvalues $E_n-iGamma_n$ of the effective Hamiltonian ${cal H}_{text{eff}}={cal H}-ipi WW^t$ describe resonant scattering from a heavy atom or quantum dot (with $E_n$ the center of the resonance and $Gamma_n$ its width). The special case in the OP where ${cal H}$ is block-off-diagonal is referred to as the case of "chiral symmetry" in the context of random-matrix theory. (The appropriate ensemble for real ${cal H}$ is the socalled "chiral orthogonal ensemble".)
Now the question in the OP is the distribution of the $Gamma_n$'s in the limit $Nrightarrowinfty$ at fixed $delta N$. The "universal" result of random-matrix theory (see section IV.A in the cited review) is that for $delta Nll N$ all $Gamma_n$'s are greater than a minimal value $Gamma_{text{min}}simeqdelta N/N$ and they accumulate near that value.
Note that the OP refers to $i$ times the eigenvalues of ${cal H}$, so this approach to the real axis corresponds to an approach to the imaginary axis in the OP.
Hence my answer to the final question of the OP, "does the spectrum approach the imaginary axis in the large-$N$ limit" is yes, it does, if the non-Hermitian perturbation has a rank $delta N$ that remains small compared to the rank of the Hermitian part. There remains, however, for any finite $N$ a gap of order $delta N/N$ that separates the "dissipative dynamics" from the unitary quantum mechanical evolution.
I show a plot that illustrates the clustering of the eigenvalues $E_n-iGamma_n$ of ${cal H}_{text{eff}}$ near the $Gamma=0$ axis, with a sharp threshold (blue horizontal line) and a gap.
In the plot $N=500$ and $delta N=50$. There is no chiral symmetry, but that would only introduce a $pm E_n$ symmetry, it would not affect the gap in the $Gamma$'s.

source: arXiv:1405.6896
edited 6 hours ago
answered 7 hours ago
Carlo BeenakkerCarlo Beenakker
77.4k9182286
77.4k9182286
$begingroup$
First, I would like to thank you for your deep insights into my question. It gives I think a lot of intuition about why this should hold. Can I however still ask you though whether the result you are referring to is rigorous?-PS: I really think what you write is very interesting for me.
$endgroup$
– Sascha
7 hours ago
1
$begingroup$
it is rigorous in the context of random-matrix theory, so for the gaussian ensembles; like all the RMT results, it is believed to hold for a much wider class of random matrices.
$endgroup$
– Carlo Beenakker
7 hours ago
$begingroup$
ah, but so it is not necessarily clear for my deterministic sequence above, right?
$endgroup$
– Sascha
7 hours ago
1
$begingroup$
not necessarily so, but keep in mind that RMT was developed for deterministic systems, such as large molecules. The randomness is introduced to make the problem tractable, RMT is believed to hold for deterministic systems if they are sufficiently complex ("chaotic dynamics" is the term). It has really a remarkably wide range of applicability, it is in fact the other way around: you have to work really hard to see behavior that deviates from the universal RMT results.
$endgroup$
– Carlo Beenakker
7 hours ago
add a comment |
$begingroup$
First, I would like to thank you for your deep insights into my question. It gives I think a lot of intuition about why this should hold. Can I however still ask you though whether the result you are referring to is rigorous?-PS: I really think what you write is very interesting for me.
$endgroup$
– Sascha
7 hours ago
1
$begingroup$
it is rigorous in the context of random-matrix theory, so for the gaussian ensembles; like all the RMT results, it is believed to hold for a much wider class of random matrices.
$endgroup$
– Carlo Beenakker
7 hours ago
$begingroup$
ah, but so it is not necessarily clear for my deterministic sequence above, right?
$endgroup$
– Sascha
7 hours ago
1
$begingroup$
not necessarily so, but keep in mind that RMT was developed for deterministic systems, such as large molecules. The randomness is introduced to make the problem tractable, RMT is believed to hold for deterministic systems if they are sufficiently complex ("chaotic dynamics" is the term). It has really a remarkably wide range of applicability, it is in fact the other way around: you have to work really hard to see behavior that deviates from the universal RMT results.
$endgroup$
– Carlo Beenakker
7 hours ago
$begingroup$
First, I would like to thank you for your deep insights into my question. It gives I think a lot of intuition about why this should hold. Can I however still ask you though whether the result you are referring to is rigorous?-PS: I really think what you write is very interesting for me.
$endgroup$
– Sascha
7 hours ago
$begingroup$
First, I would like to thank you for your deep insights into my question. It gives I think a lot of intuition about why this should hold. Can I however still ask you though whether the result you are referring to is rigorous?-PS: I really think what you write is very interesting for me.
$endgroup$
– Sascha
7 hours ago
1
1
$begingroup$
it is rigorous in the context of random-matrix theory, so for the gaussian ensembles; like all the RMT results, it is believed to hold for a much wider class of random matrices.
$endgroup$
– Carlo Beenakker
7 hours ago
$begingroup$
it is rigorous in the context of random-matrix theory, so for the gaussian ensembles; like all the RMT results, it is believed to hold for a much wider class of random matrices.
$endgroup$
– Carlo Beenakker
7 hours ago
$begingroup$
ah, but so it is not necessarily clear for my deterministic sequence above, right?
$endgroup$
– Sascha
7 hours ago
$begingroup$
ah, but so it is not necessarily clear for my deterministic sequence above, right?
$endgroup$
– Sascha
7 hours ago
1
1
$begingroup$
not necessarily so, but keep in mind that RMT was developed for deterministic systems, such as large molecules. The randomness is introduced to make the problem tractable, RMT is believed to hold for deterministic systems if they are sufficiently complex ("chaotic dynamics" is the term). It has really a remarkably wide range of applicability, it is in fact the other way around: you have to work really hard to see behavior that deviates from the universal RMT results.
$endgroup$
– Carlo Beenakker
7 hours ago
$begingroup$
not necessarily so, but keep in mind that RMT was developed for deterministic systems, such as large molecules. The randomness is introduced to make the problem tractable, RMT is believed to hold for deterministic systems if they are sufficiently complex ("chaotic dynamics" is the term). It has really a remarkably wide range of applicability, it is in fact the other way around: you have to work really hard to see behavior that deviates from the universal RMT results.
$endgroup$
– Carlo Beenakker
7 hours ago
add a comment |
Thanks for contributing an answer to MathOverflow!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmathoverflow.net%2fquestions%2f323957%2feigenvalue-estimates-for-operator-perturbations%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
$begingroup$
What is your definition of "dissipative system"? If it's simply that the spectrum has negative real part I don't see why that should be true. There are purely dissipative systems for which the spectrum is and stays entirely real
$endgroup$
– lcv
7 hours ago
$begingroup$
yes, that's true and yes that's my definition. However, in this particular case, there is a special dynamics that is mixing (the Laplacian connects all components of the system). Therefore, it is believable that it holds in this case. Please have a look at Carlo Beenakker's answer below and also the comments.
$endgroup$
– Sascha
7 hours ago
$begingroup$
See Carlo Beenakker's comment about $delta N/ N$ being finite. But this is an additional assumption. I.e. if you perturb a skewhermitian with a negative operator you may (or not) end up with some imaginary eigenvalues if the perturbation is suitably small or vanishing.
$endgroup$
– lcv
7 hours ago
$begingroup$
Sorry, I don't understand. $delta N=1$ in my case. So $delta N/N$ goes to zero. So according to him some eigenvalues should approach the imaginary axis and that is what I would like to show. I agree that this might not hold for general perturbations of skew-symmetric matrices, but the system I consider is somewhat special.-But I feel I have not understood your commet fully.
$endgroup$
– Sascha
6 hours ago