傅里叶级数
| 本條目需要擴充。 (2013年2月15日) |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

以傅里叶级数模拟非正弦曲线的方波,经常运用于电子信号的处理。
在数学中,傅里叶级数(Fourier series, /ˈfɔərieɪ/)是把类似波的函数表示成简单正弦波的方式。更正式地说,它能将任何周期函数或周期信号分解成一个(可能由无穷个元素组成的)简单振荡函数的集合,即正弦函数和余弦函数(或者,等价地使用复指数)。离散时间傅里叶变换是一个周期函数,通常用定义傅里叶级数的项进行定义。另一个应用的例子是Z变换,将傅里叶级数简化为特殊情形 |z|=1。傅里叶级数也是采样定理原始证明的核心。傅里叶级数的研究是傅里叶分析的一个分支。
目录
1 歷史
2 定义
2.1 例1:一个简单的傅里叶级数
2.2 例2:傅里叶诱导
3 延伸
3.1 希尔伯特空间的解读
4 傅里叶级数的收敛性
5 傅里叶级数的一些例子
6 参阅
7 参考文献
7.1 引用
7.2 来源
歷史
傅里叶级数得名于法国数学家约瑟夫·傅里叶(1768年–1830年),他提出任何函数都可以展开为三角级数。此前数学家如拉格朗日等已经找到了一些非周期函数的三角级数展开,而认定一個函数有三角级数展开之后,通过积分方法计算其系数的公式,欧拉、达朗贝尔和克莱羅早已发现,傅里叶的工作得到了丹尼尔·伯努利的赞助[1]。傅里叶介入三角级数用來解热传导方程,其最初论文在1807年经拉格朗日、拉普拉斯和勒讓德评審后被拒绝出版,他的现在被称为傅里葉逆轉定理的理论后来发表于1820年的《热的解析理论》中。将周期函数分解为简单振荡函数的总和的最早想法,可以追溯至公元前3世紀古代天文學家的均輪和本輪學說。
傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用。
定义
在这一节中,s(x){textstyle s(x)} 表示实变量 x{textstyle x} 的一个函数,且 s{textstyle s} 在 [x0,x0+P]{textstyle [x_{0},x_{0}+P]}上可积, x0{textstyle x_{0}} 和 P{displaystyle P} 为实数。我们将尝试用谐波关系的正弦函数的无穷和或级数来表示该区间内的 s{textstyle s} 。在区间外,级数以 P{displaystyle P} 为周期(频率为 1/P{displaystyle 1/P} )。若 s{textstyle s} 也具有该性质,则它的近似在整个实数线上有效。我们可以从有限求和(或部分和)开始:
- sN(x)=A02+∑n=1NAn⋅sin(2πnxP+ϕn),for integer N ≥ 1.{displaystyle s_{N}(x)={frac {A_{0}}{2}}+sum _{n=1}^{N}A_{n}cdot sin({tfrac {2pi nx}{P}}+phi _{n}),quad scriptstyle {text{for integer}} N geq 1.}
sN(x){displaystyle s_{N}(x)} 为周期为 P 的周期函数。运用恒等式:
- sin(2πnxP+ϕn)≡sin(ϕn)cos(2πnxP)+cos(ϕn)sin(2πnxP){displaystyle sin({tfrac {2pi nx}{P}}+phi _{n})equiv sin(phi _{n})cos({tfrac {2pi nx}{P}})+cos(phi _{n})sin({tfrac {2pi nx}{P}})}
- sin(2πnxP+ϕn)≡Re{1i⋅ei(2πnxP+ϕn)}=12i⋅ei(2πnxP+ϕn)+(12i⋅ei(2πnxP+ϕn))∗,{displaystyle sin({tfrac {2pi nx}{P}}+phi _{n})equiv {text{Re}}left{{frac {1}{i}}cdot e^{ileft({tfrac {2pi nx}{P}}+phi _{n}right)}right}={frac {1}{2i}}cdot e^{ileft({tfrac {2pi nx}{P}}+phi _{n}right)}+left({frac {1}{2i}}cdot e^{ileft({tfrac {2pi nx}{P}}+phi _{n}right)}right)^{*},}

我们还可以用这些等价形式书写这个函数:
sN(x)=a02+∑n=1N(an⏞Ansin(ϕn)cos(2πnxP)+bn⏞Ancos(ϕn)sin(2πnxP))=∑n=−NNcn⋅ei2πnxP,{displaystyle {begin{aligned}s_{N}(x)&={frac {a_{0}}{2}}+sum _{n=1}^{N}left(overbrace {a_{n}} ^{A_{n}sin(phi _{n})}cos({tfrac {2pi nx}{P}})+overbrace {b_{n}} ^{A_{n}cos(phi _{n})}sin({tfrac {2pi nx}{P}})right)\&=sum _{n=-N}^{N}c_{n}cdot e^{i{tfrac {2pi nx}{P}}},end{aligned}}} |
其中:
- cn =def {An2ieiϕn=12(an−ibn)for n>012a0for n=0c|n|∗for n<0.{displaystyle c_{n} {stackrel {mathrm {def} }{=}} {begin{cases}{frac {A_{n}}{2i}}e^{iphi _{n}}={frac {1}{2}}(a_{n}-ib_{n})&{text{for }}n>0\{frac {1}{2}}a_{0}&{text{for }}n=0\c_{|n|}^{*}&{text{for }}n<0.end{cases}}}
当系数(即傅里叶系数)以下面方式计算时:[2]
an=2P∫x0x0+Ps(x)⋅cos(2πnxP) dx{displaystyle a_{n}={frac {2}{P}}int _{x_{0}}^{x_{0}+P}s(x)cdot cos({tfrac {2pi nx}{P}}) dx}bn=2P∫x0x0+Ps(x)⋅sin(2πnxP) dx{displaystyle b_{n}={frac {2}{P}}int _{x_{0}}^{x_{0}+P}s(x)cdot sin({tfrac {2pi nx}{P}}) dx}
cn=1P∫x0x0+Ps(x)⋅e−i2πnxP dx,{displaystyle c_{n}={frac {1}{P}}int _{x_{0}}^{x_{0}+P}s(x)cdot e^{-i{tfrac {2pi nx}{P}}} dx,}
sN(x){displaystyle s_{N}(x)} 在 [x0, x0+P]{displaystyle [x_{0}, x_{0}+P]} 近似了 s(x){displaystyle s(x)} ,该近似程度会随着 N → ∞ 逐渐改善。这个无穷和 s∞(x){displaystyle s_{infty }(x)} 叫做 s{displaystyle s} 的傅里叶级数表示。在工程应用中,一般假定傅里叶级数除了在不连续点以外处处收敛,原因是工程上遇到的函数比数学家提供的这个假定的反例表现更加良好。特别地,傅里叶级数绝对收敛且一致收敛于 s(x),只要在 s(x) 的导数(或许不会处处存在)是平方可积的。[3] 如果一个函数在区间 [x0, x0+P]上是平方可积的,那么此傅里叶级数在几乎所有点都收敛于该函数。傅里叶级数的收敛性取决于函数有限数量的极大值和极小值,这就是通常称为傅里叶级数的狄利克雷条件。参见傅里叶级数的收敛性之一。对于广义函数或分布也可以用范数或弱收敛定义傅里叶系数.

一个相同幅度和频率的锯齿波的近似的可视化
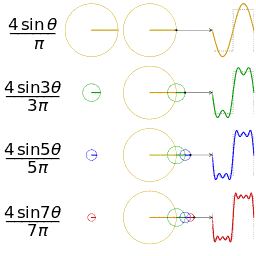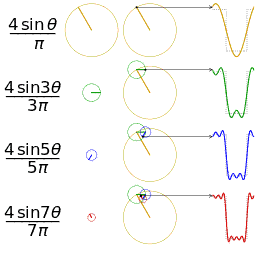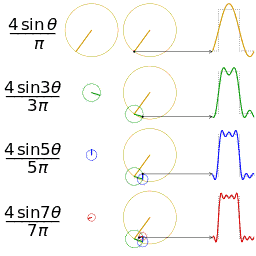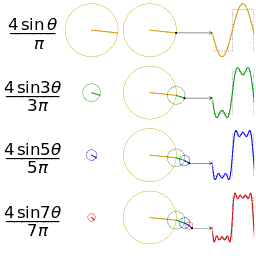
另一个分别采用傅里叶级数的前 1, 2, 3, 4 项近似方波的可视化。(可以在这里看到一个交互式的动画)
例1:一个简单的傅里叶级数

锯齿波周期函数的图

前五个部分傅里叶级数的动态图
我们现在用上面的公式给出一个简单函数的傅里叶级数展开式。考虑一个锯齿波
- s(x)=xπ,for−π<x<π,{displaystyle s(x)={frac {x}{pi }},quad mathrm {for} -pi <x<pi ,}
- s(x+2πk)=s(x),for−∞<x<∞ and k∈Z.{displaystyle s(x+2pi k)=s(x),quad mathrm {for} -infty <x<infty {text{ and }}kin mathbb {Z} .}
在这种情况下,傅里叶级数为
- an=1π∫−ππs(x)cos(nx)dx=0,n≥0.bn=1π∫−ππs(x)sin(nx)dx=−2πncos(nπ)+2π2n2sin(nπ)=2(−1)n+1πn,n≥1.{displaystyle {begin{aligned}a_{n}&{}={frac {1}{pi }}int _{-pi }^{pi }s(x)cos(nx),dx=0,quad ngeq 0.\b_{n}&{}={frac {1}{pi }}int _{-pi }^{pi }s(x)sin(nx),dx\&=-{frac {2}{pi n}}cos(npi )+{frac {2}{pi ^{2}n^{2}}}sin(npi )\&={frac {2,(-1)^{n+1}}{pi n}},quad ngeq 1.end{aligned}}}
可以证明,当 s 可微时,傅立叶级数在每个点 x 都收敛于 s(x),于是:
s(x)=a02+∑n=1∞[ancos(nx)+bnsin(nx)]=2π∑n=1∞(−1)n+1nsin(nx),forx−π∉2πZ.{displaystyle {begin{aligned}s(x)&={frac {a_{0}}{2}}+sum _{n=1}^{infty }left[a_{n}cos left(nxright)+b_{n}sin left(nxright)right]\&={frac {2}{pi }}sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n}}sin(nx),quad mathrm {for} quad x-pi notin 2pi mathbf {Z} .end{aligned}}}
()
当 x = π 时,傅里叶级数收敛于 0,为在 x = π 处 s 的左极限和右极限之和的一半。这是傅里叶级数的狄利克雷定理的特例。
这个例子为我们引出了巴塞尔问题的一种解法。
例2:傅里叶诱导

金属板内的热分布,使用傅里叶方法求解
例1中我们的函数的傅里叶级数展开式看起来不比 s(x) = x/π 简单,因此人们需要傅里叶级数的原因也就不会立即显现出来。但还有很多应用,我们举用傅里叶诱导解热方程式的例子。考虑边长为 π 米的方形金属版,坐标为 (x, y) ∈ [0, π] × [0, π]。如果板内没有热源,并且四个边中三个都保持在 0 摄氏度,而第四条边 y = π,对于 x 属于 (0, π),保持在温度梯度 T(x, π) = x 摄氏度,于是可以证明稳态热分布(或者说在很长一段时间过去后的热分布)为
- T(x,y)=2∑n=1∞(−1)n+1nsin(nx)sinh(ny)sinh(nπ).{displaystyle T(x,y)=2sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n}}sin(nx){sinh(ny) over sinh(npi )}.}
这里,sinh 为双曲正弦函数。热方程的这个解是通过将 Eq.1 的每一项乘以 sinh(ny)/sinh(nπ) 得到的。我们示例的函数 s(x) 的傅里叶级数似乎很复杂,热分布 T(x, y) 是非平凡的。函数 T 不能写成解析解。用傅里叶的方法却可以求解这个热分布问题。
延伸
希尔伯特空间的解读

正弦和餘弦形成了正交集合。正弦、餘弦及其乘積的積分,當m與n不同或二函數不同時是0(綠色和紅色區域相等抵消),僅當m和n相等並且函數相同時為π。
所谓的两个不同向量正交是指它们的内积为0,这也就意味着这两个向量之间没有任何相关性,例如,在三维欧氏空间中,互相垂直的向量之间是正交的。事实上,正交是垂直在数学上的一种抽象化和一般化。一组n个互相正交的向量必然是线性无关的,所以必然可以张成一个n维空间,也就是说,空间中的任何一个向量可以用它们来线性表出。
在希爾伯特空間釋義下,函數的集合{en = einx; n ∈ Z}是[−π, π]平方可積函數L2([−π, π])的正交基。這個空間實際上是一個希爾伯特空間,有著針對任何兩個的元素f和g的如下內積:
- ⟨f,g⟩=def12π∫−ππf(x)g(x)¯dx.{displaystyle langle f,,grangle ;{stackrel {mathrm {def} }{=}};{frac {1}{2pi }}int _{-pi }^{pi }f(x){overline {g(x)}},dx.}
三角函数族的正交性用公式表示出来就是:
- ∫−ππcos(mx)cos(nx)dx=πδmn,m,n≥1,{displaystyle int _{-pi }^{pi }cos(mx),cos(nx),dx=pi delta _{mn},quad m,ngeq 1,,}
- ∫−ππsin(mx)sin(nx)dx=πδmn,m,n≥1{displaystyle int _{-pi }^{pi }sin(mx),sin(nx),dx=pi delta _{mn},quad m,ngeq 1}
(這裡的δmn是克羅內克函數),而
- ∫−ππcos(mx)sin(nx)dx=0;{displaystyle int _{-pi }^{pi }cos(mx),sin(nx),dx=0;,}
傅里叶级数的收敛性
至今还没有判断傅里叶级数的收敛性充分必要条件,但是对于实际问题中出现的函数,有很多种判别条件可用于判断收敛性。比如x(t)的可微性或级数的一致收敛性。在闭区间上满足狄利克雷条件的函数表示成的傅里叶级数都收敛。狄利克雷条件如下:
- 在定义区间上,x(t)须绝对可积;
- 在任一有限区间中,x(t)只能取有限个极值点;
- 在任何有限区间上,x(t)只能有有限个第一类间断点。
满足以上条件的x(t)傅里叶级数都收敛,且:
- 1.当t是x(t)的连续点时,级数收敛于x(t);
- 2.当t是x(t)的间断点时,级数收敛于12[x(t−)+x(t+)]{displaystyle {frac {1}{2}}[x(t^{-})+x(t^{+})]}.
1966年,里纳特·卡尔松证明了勒贝格二次可积函数的傅立叶级数一定是几乎处处收敛的,即级数在除了一个勒贝格零测集外均收敛。
吉布斯现象:在x(t)的不可导点上,如果我们只取(1)式右边的无穷级数中的有限项作和X(t),那么X(t)在这些点上会有起伏。一个简单的例子是方波信号。
傅里叶级数的一些例子
参阅
- 离散时间傅里叶级数
- 傅里叶变换
- 维尔斯特拉斯逼近定理
参考文献
引用
^ 详见莫里斯·克莱因《古今数学思想》,第20章无穷级数,第5节三角级数;第28章十九世纪的偏微分方程,第5节热方程与傅里叶级数。
see here, pg.s 209 & 210,
^ Dorf, Richard C.; Tallarida, Ronald J. Pocket Book of Electrical Engineering Formulas 1. Boca Raton,FL: CRC Press. 1993-07-15: 171–174. ISBN 0849344735.
^ Georgi P. Tolstov. Fourier Series. Courier-Dover. 1976. ISBN 0-486-63317-9.
来源
- 书籍
- 電機電子類科《工程數學》,ISBN 978-957-584-377-9,作者 陳錫冠、曾致煌,高立出版社。
|



![{textstyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/249701ed8e93d06f1998b671ce20df9714fb018c)












![[x_{0}, x_{0}+P]](https://wikimedia.org/api/rest_v1/media/math/render/svg/46ad7364478493807dcae901dc0091bb7b6ff0fa)




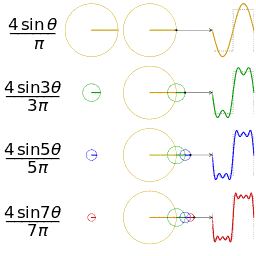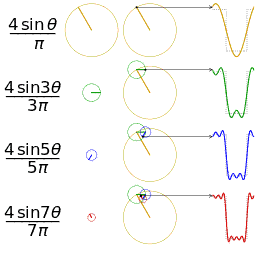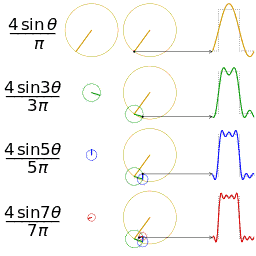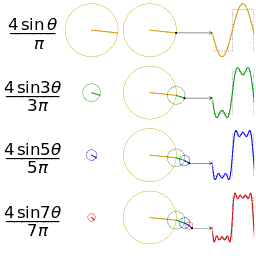



![{begin{aligned}s(x)&={frac {a_{0}}{2}}+sum _{{n=1}}^{infty }left[a_{n}cos left(nxright)+b_{n}sin left(nxright)right]\&={frac {2}{pi }}sum _{{n=1}}^{infty }{frac {(-1)^{{n+1}}}{n}}sin(nx),quad {mathrm {for}}quad x-pi notin 2pi {mathbf {Z}}.end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f7723030e9a65dde2b59bdffde660c5ac6d1a4)





![frac{1}{2}[x(t^-)+x(t^+)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/49230b01e93db8171d55b34288c6d4d8097278b3)