Jtdcftul

  本條目介紹的是数学中的函数。關於程序设计中的函数，請見“子程序”。

函数f(){displaystyle f()}就像機器或黑箱，给予输入值x{displaystyle x}便產生唯一输出值f(x){displaystyle f(x)}。

函數，在數學中，為兩集合間的一種對應關係：輸入值集合中的每項元素皆能對應唯一一項輸出值集合中的元素。例如實數x對應到其平方x²的關係就是一個函數，若以3作為此函數的輸入值，所得的輸出值便是9。

為方便起見，一般做法是以符號f,g,h{displaystyle f,g,h}等等來指代一個函數。若函數f{displaystyle f}以x{displaystyle x}作為輸入值，則其輸出值一般寫作f(x){displaystyle f(x)}，讀作f of x。上述的平方函數關係寫成數學式記為f(x)=x2{displaystyle f(x)=x^{2}}。函數的概念並不局限於數之間的映射關係，例如若定義函數Capital⁡(){displaystyle operatorname {Capital} ()}為每个国家当前的首都，那麼給予輸入值西班牙就會輸出唯一值馬德里：Capital⁡(Spain)=Madrid{displaystyle operatorname {Capital} (mathrm {Spain} )=mathrm {Madrid} }。氣溫的分佈也能用函數表達，以時間和地點作為參量輸入，以該時該地的溫度作為輸出。表達函数有多种方式，例如解析法是用数学式表达两个变量之间的对应关系，图像法是用坐标系上的函數圖形表达两个变量之间的对应关系，列表法用表格表达两个变量之间的对应关系。

現代數學中^[1]，函数所有输入值的集合被称作該函数的定义域，而其輸出值所存在的集合稱為上域或對應域。其中值域特指該函數的输出值集合，意即上域包含了值域，值域為上域的子集。通常輸入值稱作函數的參數或參量，輸出值稱作函數的值。函數將有效的輸入值變換為唯一的輸出值，同一輸入總是對應同一輸出，但反之未必成立。因此如Root(x)=±x{displaystyle mathrm {Root} (x)=pm {sqrt {x}}}這樣的表達式並沒有定義出一个函数，因为输出值有兩個可能。定義函數時需確定每一个输入值只对应唯一输出值，因此必须明确地选择一个平方根。例如定义Posroot(x)=x{displaystyle mathrm {Posroot} (x)={sqrt {x}}}，亦即对于任何非负输入值，选择其非负平方根作为函数值。

函數可以看作機器或黑箱，通常最常見的函數的參數和函數值都是數字，其對應關係用函數式表示，函數值可以通過直接將參數值代入函數式得到。f(x)=x2{displaystyle f(x)=x^{2}}，x{displaystyle x}的平方即是函數值。也可以將函數很簡單的推廣到與多個參量相關的情況。例如g(x,y)=xy{displaystyle g(x,y)=xy}有兩個參量x{displaystyle x}和y{displaystyle y}，以乘積xy{displaystyle xy}為值。將這兩個輸入看作一個有序對(x,y){displaystyle (x,y)}。g{displaystyle g}即為以這個有序對(x,y){displaystyle (x,y)}作參數的函數，而函數值是xy{displaystyle xy}。函數能被抽象定義為某種數學關係，由於其定義的一般性，在幾乎所有的數學分支都是基礎概念。一些領域中比如在λ演算中，函数可以是作為一個原始概念而不像在集合論般有所定义。在大部分的数学领域内，术语对应、映射、变换通常是函数的近义词。不過某些情況這些術語可能有別的特定意思，例如在拓扑學中一个映射有时被定义成一个连续函数。

定義

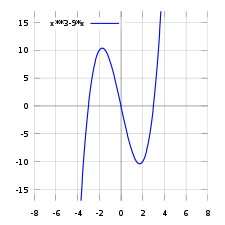
函数f的部分图像。每个实数的x都与f（x） = x³ − 9x相联系。

从输入值集合X{displaystyle X}到可能的输出值集合Y{displaystyle Y}的函数f{displaystyle f}（记作f:X→Y{displaystyle f:Xto Y}）是X{displaystyle X}与Y{displaystyle Y}的关系，满足如下条件：

1. 
   f{displaystyle f}是完全的：对集合X{displaystyle X}中任一元素x{displaystyle x}都有集合Y{displaystyle Y}中的元素y{displaystyle y}满足xfy{displaystyle xfy}（x{displaystyle x}与y{displaystyle y}是f{displaystyle f}相关的）。即，对每一个输入值，y{displaystyle y}中都有与之对应的输出值。


2. 
   f{displaystyle f}是多对一的：若f(x)=y{displaystyle f(x)=y}且f(x)=z{displaystyle f(x)=z}，则y=z{displaystyle y=z}。即，多个输入可以映射到一个输出，但一个输入不能映射到多个输出。

定义域中任一x{displaystyle x}在到達域中唯一对应的y{displaystyle y}记为f(x){displaystyle f(x)}。

比上面定义更简明的表述如下：从X{displaystyle X}映射到Y{displaystyle Y}的函数f{displaystyle f}是X{displaystyle X}与Y{displaystyle Y}的直积X×Y{displaystyle Xtimes Y}的子集。X{displaystyle X}中任一x{displaystyle x}都与Y{displaystyle Y}中的y{displaystyle y}唯一对应，且有序对(x,y){displaystyle (x,y)}属于f{displaystyle f}。

X{displaystyle X}与Y{displaystyle Y}的关系若满足条件（1），则为多值函数。函数都是多值函数，但多值函数不都是函数。X{displaystyle X}与Y{displaystyle Y}的关系若满足条件（2），则为偏函数。函数都是偏函数，但偏函数不都是函数。除非特别指明，本條目中的“函数”总是指同时满足以上两个条件的关系。
考虑如下例子：

（1）一對多。X中的元素3与Y中的两个元素b和c相关。因此这是多值函数，而不是函数。

（2）多对一或一對一。X的元素1未与Y的任一元素相关。因此这是偏函数，而不是函数。

（3）完全對應且多对一，因此这是从X到Y的函数。此函数可以表示为.mw-parser-output .serif{font-family:Times,serif}
f ={(1, d), (2, d), (3, c)}，或f(x)={d,if x=1d,if x=2c,if x=3{displaystyle f(x)=left{{begin{matrix}d,&{mbox{if }}x=1\d,&{mbox{if }}x=2\c,&{mbox{if }}x=3end{matrix}}right.}

历史

函数这个数学名词是莱布尼兹在1694年开始使用的，用來描述跟曲线相关的一個量，如曲线的斜率或者曲线上的某一点。莱布尼兹所指的函数现在被称作可导函数，数学家之外的普通人一般接触到的函数即属此类。对于可导函数可以讨论它的极限和导数，此两者描述了函数输出值的变化同输入值变化的关系，是微积分学的基础。中文的“函数”一词由清朝数学家李善兰译出。其《代数学》书中解释：“凡此變數中函（包含）彼變數者，則此為彼之函數”。

• 1718年，約翰·伯努利把函数定义为“一个变量的函数是指由这个变量和常量以任何一种方式组成的一种量。”


• 1748年，伯努利的学生欧拉在《无穷分析引论》一书中说：“一个变量的函数是由该变量和一些数或常量以任何一种方式构成的解析表达式”，例如f(x)=sin⁡(x)+x3{displaystyle f(x)=sin(x)+x^{3}}。


• 1775年，欧拉在《微分学原理》一书中又提出了函数的一个定义：“如果某些量以如下方式依赖于另一些量，即当后者变化时，前者本身也发生变化，则称前一些量是后一些量的函数。”


• 19世纪的数学家开始对数学的各个分支進行形式化。维尔斯特拉斯倡議将微积分学建立在算术，而不是几何的基础上，這種主張較趋向于欧拉的定义。


• 函数的定义得以擴展之後，数学家便能对一些“奇怪”的数学对象进行研究，例如處處不可导的连续函数。这些函数曾经被认为只具有理论价值，迟至20世纪初时它们仍被视作“怪物”。稍后，人们发现这些函数在对如布朗运动之类的物理现象进行建模时有重要的作用。


• 到19世纪末，数学家开始尝试利用集合论来進行数学的形式化。他们试图将每一個数学对象都定义为集合。狄利克雷给出了现代正式的函数定义（参见下文#正式定义）。在他的定義下，函数被视作数学关系的特例。然而对于实际应用的情况，现代定义和欧拉定义的区别可以忽略不计。

表示方法

• 描述法


• 表格法


• 公式法

函数的判别

除了利用函数的定义之外，还可以利用竖直判别法，即函数的图形与任何一条平行于 y 轴的直线不能有一个以上的交点。

单射、满射与双射函数

• 
  单射函数，将不同的輸入值映射到不同的函數值。即：若x{displaystyle x}和y{displaystyle y}属于定义域，则仅当x=y{displaystyle x=y}时有f(x)=f(y){displaystyle f(x)=f(y)}。


• 
  满射函数，其值域即为其到達域。即：对於映射f{displaystyle f}的到達域中之任意y{displaystyle y}，都存在至少一个x{displaystyle x}满足f(x)=y{displaystyle f(x)=y}。


• 
  双射函数，既是单射的又是满射的函數。也叫一一对应、對射。双射函数经常被用于表明集合X{displaystyle X}和Y{displaystyle Y}是等势的，即有一样的基数。如果在两个集合之间可以建立一个一一对应，则说这两个集合等势。

定义域与值域、陪域

• 定义域：原像集，自变量的取值集合。


• 值域：像集，因变量的取值集合。


• 陪域：值域所属的全集。

像和原像

元素x∈X{displaystyle xin X}在f{displaystyle f}之下的像就是f(x){displaystyle f(x)}。

子集A⊂X{displaystyle Asubset X}在f{displaystyle f}之下的像，是以A{displaystyle A}的元素的像所組成的集合，為Y{displaystyle Y}的一個子集，即

f(A):={f(x):x∈A}{displaystyle f(A):={f(x):xin A}}。

注意f{displaystyle f}的值域就是定義域X{displaystyle X}的像f(X){displaystyle f(X)}。在#正式定义一節的最後例子中，{2,3}{displaystyle {2,3}}在f{displaystyle f}的像是f({2,3}={c,d}{displaystyle f({2,3}={c,d}}，而f{displaystyle f}的值域是{c,d}{displaystyle {c,d}}。

根據此定義，f{displaystyle f}可引申成為由X{displaystyle X}的幂集（由X{displaystyle X}的子集組成的集）到Y{displaystyle Y}的幂集之函數，亦記作f{displaystyle f}。

子集B⊂Y{displaystyle Bsubset Y}在f{displaystyle f}的原像（或逆像）是如下定義的X{displaystyle X}的子集：

f−1(B):={x∈X:f(x)∈B}{displaystyle f^{-1}(B):={xin X:f(x)in B}}。

沿用同一例子，我們可以看到{a,b}{displaystyle {a,b}}的原像是f−1({a,b})=∅{displaystyle f^{-1}({a,b})=varnothing }，即空集。

根據此定義，f−1(x){displaystyle f^{-1}(x)}是由Y{displaystyle Y}的幂集到X{displaystyle X}的幂集之函數。

以下是f{displaystyle f}及f−1{displaystyle f^{-1}}的一些特性：

• 
  f(A1∪A2)=f(A1)∪f(A2){displaystyle f(A_{1}cup A_{2})=f(A_{1})cup f(A_{2})}；


• 
  f(A1∩A2)⊆f(A1)∩f(A2){displaystyle f(A_{1}cap A_{2})subseteq f(A_{1})cap f(A_{2})}；


• 
  f(B1∪B2)=f−1(B1)∪f−1(B2){displaystyle f(B_{1}cup B_{2})=f^{-1}(B_{1})cup f^{-1}(B_{2})}；


• 
  f−1(B1∩B2)=f−1(B1)∩f−1(B2){displaystyle f^{-1}(B_{1}cap B_{2})=f^{-1}(B_{1})cap f^{-1}(B_{2})}；


• 
  f−1(f(B))⊆B{displaystyle f^{-1}(f(B))subseteq B}；


• 
  f−1(f(A))⊇A{displaystyle f^{-1}(f(A))supseteq A}。

這些特性適合定義域的任意子集A,A1{displaystyle A,A_{1}}及A2{displaystyle A_{2}}和到達域的任意子集B,B1{displaystyle B,B_{1}}及B2{displaystyle B_{2}}，甚至可推廣到任意子集群的交集和并集。

函数图形

@media all and (max-width:720px){body.skin-minerva .mw-parser-output div.mw-graph{min-width:auto!important;max-width:100%;overflow-x:auto;overflow-y:visible}}

sin(x)等函數的圖形。

函数f{displaystyle f}在平面上的图形是点对(x,f(x)){displaystyle (x,f(x))}的集合，其中x{displaystyle x}取遍定义域上的所有成员。函数图形可以帮助理解证明一些定理。
注意函数图形可以有兩個定義：一是三元組(X,Y,G){displaystyle (X,Y,G)}，其中X{displaystyle X}是函數的定義域，Y{displaystyle Y}是函數的到達域，G{displaystyle G}是關係的圖；二是索性以關係的圖定義。用第二個定義則函数f{displaystyle f}等於其图形。

函数範例

• 首都之於国家（若不把多首都国[1] 计算在内)。


• 每个自然数n{displaystyle n}的平方n2{displaystyle n^{2}}是n{displaystyle n}的函數。


• 
  對數函數。ln⁡x{displaystyle ln x}是正实数x{displaystyle x}的函數。注意，雖然可以把對數函數推廣到複數情況，但結果就不是函數了，而是多值函數。


• 對每个在R2{displaystyle mathbb {R} ^{2}}平面上的点，其和原点(0,0){displaystyle (0,0)}的距离是確定的。

常用的数学函数包括多项式函數、根式函數、冪函數、对数函數、有理函数、三角函数、反三角函數等。它们都是初等函数。非初等函数（或特殊函数）包括伽马函數和贝塞尔函数等。

函數的特性

函數可分為

• 
  奇函數或偶函數
  


• 
  連續函數或不連續函數
  


• 
  實函數或虛函數
  


• 
  純量函數或向量函數
  


• 
  单调增函数或单调减函数
  

分段函数

分段函数（Deutsch：Abschnittsweise definierte Funktion），在定义域内不同部分上，有不同的解析表达式，这样的函数通常叫分段函数。

复合函数

函數f:X→Y{displaystyle f:Xto Y}及g:Y→Z{displaystyle g:Yto Z}的複合函數是

g∘f:X→Z:f(g∘f)(x)=g(f(x)){displaystyle gcirc f:Xto Z:f(gcirc f)(x)=g(f(x))}。

舉例，飛機在t{displaystyle t}时刻的高度是h(t){displaystyle h(t)}，而高度x{displaystyle x}处的氧气浓度是c(x){displaystyle c(x)}，則在t{displaystyle t}时刻飛機周围的氧氣濃度是
(c∘h)(t){displaystyle (ccirc h)(t)}

若Y⊂X{displaystyle Ysubset X}則
f{displaystyle f}可自我複合；此時複合函數可記作f2{displaystyle f^{2}}（不要與三角學的符號混淆）。函數的幂的定義是對自然數n{displaystyle n}有

fn+1=fn∘f=f∘fn{displaystyle f^{n+1}=f^{n}circ f=fcirc f^{n}}

反函数

y=x2{displaystyle y=x^{2}}與y=x{displaystyle y={sqrt {x}}}互為反函数，並且於鏡射於軸y=x{displaystyle y=x}上。

对一个函数f: X→Y，若值域Y中任何一个元素y的原象是唯一的，那么这个函数就被称为是双射的。对任意的y∈Y到它的原象ƒ⁻¹(y)的映射，我们称之为f的反函数，记为f⁻¹。

举一个反函数的例子，比如ƒ(x) = x³，它的反函数是ƒ⁻¹(x) = x3{displaystyle {sqrt[{3}]{x}}} 。同样，2x的反函数是x/2。反函数是一个函数，它能够“抵消”它的原函数，并具有和原函数相同的单调性。参见逆映射。

函數的限制及擴張

給出Y{displaystyle Y}的子集X{displaystyle X}以及函數

f:Y→Z{displaystyle f:Yrightarrow Z}，

則

f|X:X→Z{displaystyle f|_{X}:Xrightarrow Z}

f|X(x)=f(x){displaystyle f|_{X}(x)=f(x)}

稱為f{displaystyle f}在X{displaystyle X}的限制。

反之，若給出函數

g:X→Z{displaystyle g:Xto Z}

當一個定義在Y{displaystyle Y}的函數f:Y→Z{displaystyle f:Yto Z}有f|X=g{displaystyle f|_{X}=g}，f{displaystyle f}就是g{displaystyle g}的擴張。

点态运算

設函數f: X → R及g: X → R有X為共同的定義域及環R為共同的到達域。我們可以定義“函數和”f + g: X → R及“函數積”f×g：X → R如下：

(f + g)(x) := ƒ(x) + g(x);

f×g(x) := ƒ(x)×g(x);

对于所有X中的x。

這樣子我們得出一個函數組成的環。這是一個抽象性擴張的例子，由此我們從較簡單的結構得出更複雜的。

若然用別的代數結構A代替R，得出的由X到A的函數集會類似地擁有和A相同的代數結構。

歧義函數

歧義函數，也称多值函数，指有輸出值多於一個的情況。例如，4的平方根可以是2或者-2，而兩者的平方皆是4。

嚴格來說，歧義函數不完全算是函數，因為數學函數的定義對於一個輸入值只能有唯一一個輸出值。實際上，這樣的「函數」通常被稱為關係式。复变函数理论采用黎曼面处理函数多值的困境。

一元函数

设 D 是实数集 R 中的非空子集，称映射 f : D -> R 为定义在 D 上的一元函数。

多元函数

多元函数（n-元函數）是指輸入值為n-元組的函數。或者說，若一函數的輸入值域為n個集合的笛卡尔积的子集，這函數就是n-元函數。例如，距離函數dist((x,y))是一個二元函數，輸入值是由兩個點組成的序對。另外，多複變函數（即輸入值為複數的多元組）是一個重要的數學課題。

在抽象代數中，運算元其實都是函數，如乘法"*"是個二元函數：當我們寫x*y時，其實是用上了*(x,y)的中綴表示法。

函數式程序设计是一個以函數概念為中心的重要理論範式，其中的运算对象为多元函数，基本语法基于λ演算，而函数的复合则采用代换来完成。特别地，通过一种称为柯里化的变换，可将多元函数变换为一元函数。

可计算和不可计算函数

所有从整数到整数的可计算函数的个数是可数的，这是因为所有可能的算法个数是可数的。从整数到整数的函数个数要更多些－和实数个数一样多，也就是说是等势的。这说明有些从整数到整数的函数是不可计算的。关于不可计算函数，请参看停机问题和莱斯定理，OEIS中有一個經典的例子： A102288。

范畴論觀點下的函数

在范畴论中，函数的槪念被推廣為態射的槪念。

一個范畴包括一組物件與一組態射，每一個態射是個三元组(X, Y, f)，X稱為源物件（定義域的類比），Y稱為目標物件（到達域的類比），而源物件与目標物件是范畴內的物件。基于这种解释，可以把函数看作集合范畴裡面的態射。

參考文獻

• 
  Visual Calculus by Lawrence S. Husch, 田納西大學（2001年）

外部链接

• NIST數學函數


• 
  mysuc.com，经典函数示例


• 
  Wolfram函数网站，汇集了各数学函数的公式和图像


• Was ist eine Funktion?


• 
  xFunctions一个多功能的Java小程序，可以显示函数的图像，既可以在线使用，也可以下载运行。


• FooPlot


• Curvas