矩阵
body.skin-minerva .mw-parser-output table.infobox caption{text-align:center}
| 「m-by-n matrix」的各地常用別名 | |
|---|---|
| 中国大陸 | m行n列矩阵 |
| 臺灣 | m列n行矩陣 |
| 港澳 | - |
| 「横向的一条线(row)」的各地常用別名 | |
|---|---|
| 中国大陸 | 行 |
| 臺灣 | 列 |
| 港澳 | - |
| 「纵向的一条线(column)」的各地常用別名 | |
|---|---|
| 中国大陸 | 列 |
| 臺灣 | 行 |
| 港澳 | - |

矩陣
數學上,一個m×n{displaystyle mtimes n}的矩陣是一个由m{displaystyle m}行(row)n{displaystyle n}列(column)元素排列成的矩形阵列。矩陣里的元素可以是数字、符号或数学式。以下是一个由6个数字元素构成的2行3列的矩阵:
大小相同(行数列数都相同)的矩阵之间可以相互加减,具体是对每个位置上的元素做加减法。矩阵的乘法则较为复杂。两个矩阵可以相乘,当且仅当第一个矩阵的列数等于第二个矩阵的行数。矩阵的乘法满足结合律和分配律,但不满足交换律。
矩阵的一个重要用途是解线性方程组。线性方程组中未知量的系数可以排成一个矩阵,加上常数项,则称为增广矩阵。另一个重要用途是表示线性变换,即是诸如f(x)=4x{displaystyle f(x)=4x}之类的線性函數的推广。设定基底后,某个向量v{displaystyle mathrm {v} }可以表示为m×1{displaystyle mtimes 1}的矩阵,而线性变换f{displaystyle f}可以表示为列数为m{displaystyle m}的矩阵A{displaystyle A},使得经过变换后得到的向量f(v){displaystyle f(mathrm {v} )}可以表示成Av{displaystyle Amathrm {v} }的形式。矩阵的特征值和特征向量可以揭示线性变换的深层特性。
矩陣是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。在物理学中,矩阵于力学、电路学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。对一些应用广泛而形式特殊的矩阵,例如稀疏矩阵和准对角矩阵,有特定的快速运算算法。关于矩阵相关理论的发展和应用,請參考矩陣理論。在天体物理、量子力学等领域,也会出现无穷维的矩阵,是矩阵的一种推广。
目录
1 词源
2 發展
3 定义
3.1 标记
4 矩陣的基本運算
5 矩阵乘法
5.1 线性方程组
5.2 线性变换
6 方块矩阵
6.1 行列式
6.2 特征值与特征向量
6.3 对称
6.4 正定性
7 矩阵的计算
7.1 矩阵分解
8 矩阵的推广
8.1 一般域和环上的矩阵
8.2 矩阵与线性变换
8.3 矩阵群
8.4 无限维矩阵
8.5 空矩阵
8.6 分塊矩陣
9 应用
9.1 图论
9.2 数学分析
9.3 概率论与统计
9.4 物理学上的对称性及线性变换
9.5 量子态的线性组合
9.6 简正模式
9.7 幾何光學
9.8 電子學
10 参见
11 注释与参考
11.1 脚注
11.2 参考文献
12 外部链接
词源
中文中矩阵的概念最早见于1922年。1922年,北京师范大学附属中学數學老師程廷熙在一篇介绍文章中将矩阵译为“纵横阵”。1925年,科学名词审查会算学名词审查组在《科学》第十卷第四期刊登的审定名词表中,矩阵被翻译为“矩阵式”,方块矩阵翻译为“方阵式”,而各类矩阵如“正交矩阵”、“伴随矩阵”中的“矩阵”则被翻译为“方阵”。1935年,中国数学会审查后,中华民国教育部审定的《数学名词》(并“通令全国各院校一律遵用,以昭划一”)中,“矩阵”作为译名首次出现。1938年,曹惠群在接受科学名词审查会委托就数学名词加以校订的《算学名词汇编》中,认为应当的译名是“长方阵”。中华人民共和国成立后编订的《数学名词》中,则将译名定为“(矩)阵”。1993年,中国自然科学名词审定委员会公布的《数学名词》中,“矩阵”被定为正式译名,并沿用至今[1]。
發展
作為解決線性方程的工具,矩陣也有不短的歷史。成书最迟在东汉前期的《九章算术》中,已经出现过以矩阵形式表示线性方程组系数以解方程的图例,可算作是矩阵的雏形[2]。矩阵正式作为数学中的研究对象出现,则是在行列式的研究发展起来后。逻辑上,矩阵的概念先于行列式,但在实际的历史上则恰好相反。日本数学家关孝和(1683年)与微積分的發現者之一戈特弗里德·威廉·萊布尼茨(1693年)近乎同时地独立建立了行列式論。其后行列式作为解线性方程组的工具逐步发展。1750年,加布里尔·克拉默发现了克莱姆法则[3]。

阿瑟·凯莱被认为是矩阵论的奠基人
进入十九世纪后,行列式的研究进一步发展,矩阵的概念也应运而生。奧古斯丁·路易·柯西是最早将行列式排成方阵并将其元素用双重下标表示的数学家。他还在1829年就在行列式的框架中证明了实对称矩阵特征根为实数的结论[4]。其后,詹姆斯·約瑟夫·西爾維斯特注意到,在作为行列式的计算形式以外,将数以行和列的形式作出的矩形排列本身也是值得研究的。在他希望引用数的矩形阵列而又不能用行列式来形容的时候,就用“matrix”一词来形容[5]。而在此之前,数学家已经开始将增广矩阵作为独立的对象引用了。西尔维斯特使用“matrix”一词是因为他希望讨论行列式的子式,即将矩阵的某几行和某几列的共同元素取出来排成的矩阵的行列式,所以实际上“matrix”被他看做是生成各种子式的“母体”:
.mw-parser-output .templatequote{margin-top:0;overflow:hidden}.mw-parser-output .templatequote .templatequotecite{line-height:1em;text-align:left;padding-left:2em;margin-top:0}.mw-parser-output .templatequote .templatequotecite cite{font-size:small}
我在先前的文章中将矩形排布的序列称为“Matrix”,盖因从中可以产生出各种不同的行列式,就如由同一个母体的子宫中孕育出来一样。[6]
阿瑟·凯莱被公认为矩阵论的奠基人[7]。他开始将矩阵作为独立的数学对象研究时,许多与矩阵有关的性质已经在行列式的研究中被发现了,这也使得凯莱认为矩阵的引进是十分自然的。他说:“我决然不是通过四元数而获得矩阵概念的;它或是直接从行列式的概念而来,或是作为一个表达线性方程组的方便方法而来的。[8]”他从1858年开始,发表了《矩阵论的研究报告》等一系列关于矩阵的专门论文[9][10],研究了矩阵的运算律、矩阵的逆以及转置和特征多项式方程。凯莱还提出了凯莱-哈密尔顿定理,并验证了3×3矩阵的情况,又说进一步的证明是不必要的。哈密尔顿证明了4×4矩阵的情况,而一般情况下的证明是弗罗贝尼乌斯于1898年给出的[11]。
此后更多的数学家开始对矩阵进行研究。埃尔米特证明了如果矩阵等于其复共轭转置,则特征根为实数。这种矩阵后来被称为埃尔米特矩阵[12]。弗罗贝尼乌斯对矩阵的特征方程、特征根、矩阵的秩、正交矩阵、矩阵方程等方面做了大量工作。1878年,在引进了不变因子、初等因子等概念的同时,弗罗贝尼乌斯给出了正交矩阵、相似矩阵和合同矩阵的概念。同年,他探讨了矩阵的最小多项式(最小方程)问题。1894年的论文中,他讨论了矩阵理论和四元数理论的关系。1896年,他给出了凯莱-哈密尔顿定理的完整证明[1]。矩阵理论在19世纪沿着两个方向发展,分别是作为抽象代数结构和作为代数工具描述几何空间的线性变换。矩阵理论为群论和不变量理论的发展。
无限维矩阵的研究始于1884年。庞加莱在两篇不严谨地使用了无限维矩阵和行列式理论的文章后开始了对这一方面的专门研究[1]。1906年,希尔伯特引入无限二次型(相当于无限维矩阵)对积分方程进行研究,极大地促进了无限维矩阵的研究。在此基础上,施密茨、赫林格和特普利茨发展出算子理论,而无限维矩阵成为了研究函数空间算子的有力工具[1]。
定义
将一些元素排列成若干行,每行放上相同数量的元素,就是一个矩阵。这里说的元素可以是数字,例如以下的矩阵:
- A=[91351117392607]{displaystyle mathbf {A} ={begin{bmatrix}9&13&5\1&11&7\3&9&2\6&0&7end{bmatrix}}}
排列成的形状是矩形,所以称为矩阵。在中國大陸,橫向的元素组称為「行」,縱向称為「列」,而在台灣則相反,橫向称為「列」,縱向称為「行」[13]。矩阵一般用大写拉丁字母表示,需要具体写出其中元素时,一般用方括号或圆括号括起。以上的矩阵A{displaystyle mathbf {A} }是一个4行3列的矩阵。
行数是1或列数是1的矩阵又可分别称为行向量和列向量。这是因为一个向量可以表示成行数或列数是1的矩阵形式。矩阵的任一行(列)都是一个行(列)向量,例如矩阵A{displaystyle mathbf {A} }的第一行 [9135]{displaystyle {begin{bmatrix}9&13&5end{bmatrix}}}就是一个行向量。行(列)向量可以看成一个向量,因此可以称矩阵的两行(列)相等,或者某一行等于某一列,表示其对应的向量相等。
标记
一个矩阵A{displaystyle mathbf {A} }從左上角數起的第i{displaystyle i}行第j{displaystyle j}列上的元素称为第i,j{displaystyle i,j}項,通常记为Ai,j{displaystyle mathbf {A} _{i,j}}、Aij{displaystyle mathbf {A} _{ij}}、aij{displaystyle mathrm {a} _{ij}}或A[i,j]{displaystyle mathbf {A} _{[i,j]}}。在上述例子中A[4,3]=7{displaystyle mathbf {A} _{[4,3]}=7}。如果不知道矩阵A{displaystyle mathbf {A} }的具体元素,通常也会将它记成A[aij]m×n{displaystyle mathbf {A} [mathbf {a} _{ij}]_{mtimes n}}或A[ai,j]m×n{displaystyle mathbf {A} [mathbf {a} _{i,j}]_{mtimes n}}。反之,如果A{displaystyle mathbf {A} }的元素可以写成只与其行数i{displaystyle i}和列数j{displaystyle j}有关的统一函数f{displaystyle f},那么也可以用A=[f(i,j)]m×n{displaystyle mathbf {A} =left[f(i,j)right]_{mtimes n}}作为A{displaystyle mathbf {A} }的简写。例如B=[i+2j]2×3{displaystyle mathbf {B} =left[i+2jright]_{2times 3}}是矩阵
- B=[357468]{displaystyle mathbf {B} ={begin{bmatrix}3&5&7\4&6&8end{bmatrix}}}
的简写。要注意的是,一些计算机编程语言中,会将第1行(列)称为第0行(列),从而对矩阵的写法产生影响,比如矩阵B{displaystyle mathbf {B} }就要改写成B=[i+2j+3]2×3{displaystyle mathbf {B} =left[i+2j+3right]_{2times 3}}。
矩阵的元素可以是数字、符号或数学表达式。一般为了支持矩阵的运算,矩阵的元素之间应当能做加减法和乘法,所以是某个环里的元素。最常见的是元素属于实数域或复数域的矩阵,简称为实矩阵和复矩阵。更一般的情况下,矩阵的元素可以是由一个环中的元素排成。给定一个环R{displaystyle mathbf {R} },所有由R{displaystyle mathbf {R} }中元素排成的m×n{displaystyle mtimes n}矩陣的集合写作M(m,n,R){displaystyle {mathcal {M}}(m,n,mathbf {R} )}或Mm×n(R){displaystyle {mathcal {M}}_{mtimes n}(mathbf {R} )}。若m=n{displaystyle m=n},則通常記以M(m,R){displaystyle {mathcal {M}}(m,mathbf {R} )}或Mm(R){displaystyle {mathcal {M}}_{m}(mathbf {R} )},称其为n{displaystyle n}维矩阵或方阵。
矩陣的基本運算
矩阵的最基本运算包括矩阵加(减)法,数乘和转置运算。被称为“矩阵加法”、“数乘”和“转置”的运算不止一种[14],其中最基本最常用的定义如下:
| 运算 | 定义 | 例子 |
|---|---|---|
| 加(减)法 | m×n{displaystyle mtimes n}矩陣A{displaystyle mathbf {A} }和B{displaystyle mathbf {B} }的和(差):A±B{displaystyle mathbf {A} pm mathbf {B} }為一个m×n{displaystyle mtimes n}矩陣,其中每个元素是A{displaystyle mathbf {A} }和B{displaystyle mathbf {B} }相应元素的和(差),
| [131100]+[005750]=[1+03+01+51+70+50+0]=[136850]{displaystyle {begin{bmatrix}1&3&1\1&0&0end{bmatrix}}+{begin{bmatrix}0&0&5\7&5&0end{bmatrix}}={begin{bmatrix}1+0&3+0&1+5\1+7&0+5&0+0end{bmatrix}}={begin{bmatrix}1&3&6\8&5&0end{bmatrix}}} |
| 数乘 | 标量c{displaystyle c}与矩陣A{displaystyle mathbf {A} }的数乘:cA{displaystyle cmathbf {A} }的每个元素是A{displaystyle mathbf {A} }的相应元素与c{displaystyle c}的乘积,
| 2⋅[18−34−25]=[2⋅12⋅82⋅(−3)2⋅42⋅(−2)2⋅5]=[216−68−410]{displaystyle 2cdot {begin{bmatrix}1&8&-3\4&-2&5end{bmatrix}}={begin{bmatrix}2cdot 1&2cdot 8&2cdot (-3)\2cdot 4&2cdot (-2)&2cdot 5end{bmatrix}}={begin{bmatrix}2&16&-6\8&-4&10end{bmatrix}}} |
| 转置 | m×n{displaystyle mtimes n}矩阵A{displaystyle mathbf {A} }的转置是一个n×m{displaystyle ntimes m}的矩阵,记为AT{displaystyle mathbf {A} ^{mathrm {T} }}(有些书中也记为Atr{displaystyle mathbf {A} ^{mathrm {tr} }}或tA{displaystyle ^{mathrm {t} }mathbf {A} }、A′{displaystyle mathbf {A} '}),其中的第i{displaystyle i}个行向量是原矩阵A{displaystyle mathbf {A} }的第i{displaystyle i}个列向量;或者说,转置矩阵AT{displaystyle mathbf {A} ^{mathrm {T} }}第i{displaystyle i}行第j{displaystyle j}列的元素是原矩阵A{displaystyle mathbf {A} }第j{displaystyle j}行第i{displaystyle i}列的元素,
| [1230−67]T=[102−637]{displaystyle {begin{bmatrix}1&2&3\0&-6&7end{bmatrix}}^{T}={begin{bmatrix}1&0\2&-6\3&7end{bmatrix}}} |
矩阵的加法运算满足交换律:A+B=B+A{displaystyle mathbf {A} +mathbf {B} =mathbf {B} +mathbf {A} }[15]。矩阵的转置和数乘运算对加法满足分配律:
- (A+B)T=AT+BT{displaystyle (mathbf {A} +mathbf {B} )^{mathrm {T} }=mathbf {A} ^{mathrm {T} }+mathbf {B} ^{mathrm {T} }}
- c(A+B)=cA+cB{displaystyle c(mathbf {A} +mathbf {B} )=cmathbf {A} +cmathbf {B} }
矩阵加法和数乘兩種運算使得M(m,n,R){displaystyle {mathcal {M}}(m,n,mathbb {R} )}成為一个mn{displaystyle mn}维的實數線性空間。而转置和数乘运算满足类似于结合律的规律:
- c(AT)=c(A)T{displaystyle c(mathbf {A} ^{mathrm {T} })=c(mathbf {A} )^{mathrm {T} }}
矩阵也有类似行列式的初等变换,即对矩阵的某些行和某些列进行三类操作:交换两行(列),将一行(列)的每个元素都乘以一个固定的量,以及将一行(列)的每个元素乘以一个固定的量之后加到另一行(列)的相应元素上。这些操作在求其逆矩阵时有用。
矩阵乘法
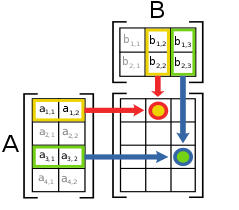
矩阵A和B相乘得到AB的示意图
两个矩阵的乘法仅当第一个矩陣A{displaystyle mathbf {A} }的列數(column)和另一个矩阵B{displaystyle mathbf {B} }的行數(row)相等时才能定义。如A{displaystyle mathbf {A} }是m×n{displaystyle mtimes n}矩陣和B{displaystyle mathbf {B} }是n×p{displaystyle ntimes p}矩陣,它們的乘積AB{displaystyle mathbf {AB} }是一個m×p{displaystyle mtimes p}矩陣,它的一个元素
- [AB]i,j=Ai,1B1,j+Ai,2B2,j+⋯+Ai,nBn,j=∑r=1nAi,rBr,j{displaystyle [mathbf {AB} ]_{i,j}=A_{i,1}B_{1,j}+A_{i,2}B_{2,j}+cdots +A_{i,n}B_{n,j}=sum _{r=1}^{n}A_{i,r}B_{r,j}}
其中1≤i≤m, 1≤j≤p′{displaystyle 1leq ileq m, 1leq jleq p'}'[16]。
例如
- [102−131]×[312110]=[(1×3+0×2+2×1)(1×1+0×1+2×0)(−1×3+3×2+1×1)(−1×1+3×1+1×0)]=[5142]{displaystyle {begin{bmatrix}1&0&2\-1&3&1\end{bmatrix}}times {begin{bmatrix}3&1\2&1\1&0end{bmatrix}}={begin{bmatrix}(1times 3+0times 2+2times 1)&(1times 1+0times 1+2times 0)\(-1times 3+3times 2+1times 1)&(-1times 1+3times 1+1times 0)\end{bmatrix}}={begin{bmatrix}5&1\4&2\end{bmatrix}}}
矩阵的乘法满足结合律和对矩阵加法的分配律(左分配律和右分配律):
- 结合律:(AB)C=A(BC){displaystyle (mathbf {AB} )mathbf {C} =mathbf {A} (mathbf {BC} )}
- 左分配律:(A+B)C=AC+BC{displaystyle (mathbf {A} +mathbf {B} )mathbf {C} =mathbf {AC} +mathbf {BC} }
- 右分配律:C(A + B) ={displaystyle =} CA + CB.
矩阵的乘法与数乘运算之间也满足类似结合律的规律;与转置之间则满足倒置的分配律。
- c(AB)=(cA)B=A(cB){displaystyle c(mathbf {AB} )=(cmathbf {A} )mathbf {B} =mathbf {A} (cmathbf {B} )}
- (AB)T=BTAT{displaystyle (mathbf {AB} )^{mathrm {T} }=mathbf {B} ^{mathrm {T} }mathbf {A} ^{mathrm {T} }}
矩阵乘法不满足交换律。一般来说,矩陣A{displaystyle mathbf {A} }及B{displaystyle mathbf {B} }的乘积AB{displaystyle mathbf {AB} }存在,但BA{displaystyle mathbf {BA} }不一定存在,即使存在,大多数时候AB≠BA{displaystyle mathbf {AB} neq mathbf {BA} }。比如下面的例子:
[1234][0100]=[0103],[0100][1234]=[3400]{displaystyle {begin{bmatrix}1&2\3&4\end{bmatrix}}{begin{bmatrix}0&1\0&0\end{bmatrix}}={begin{bmatrix}0&1\0&3\end{bmatrix}},qquad quad {begin{bmatrix}0&1\0&0\end{bmatrix}}{begin{bmatrix}1&2\3&4\end{bmatrix}}={begin{bmatrix}3&4\0&0\end{bmatrix}}}。
这一特性使得矩阵代数与常见的一些数域(有理数、实数、复数)以及环(多项式环、整数环)都不同。给定一个n{displaystyle n}维的方块矩阵A{displaystyle mathbf {A} },与A{displaystyle mathbf {A} }交换的所有方块矩阵构成一个环,称为A{displaystyle mathbf {A} }的交换子环。这些矩阵也构成M(n,R){displaystyle {mathcal {M}}(n,mathbb {R} )}的一个子空间,称为A{displaystyle mathbf {A} }的可交换空间[17]。与M(n,R){displaystyle {mathcal {M}}(n,mathbb {R} )}中所有矩阵交换的矩阵只有形如λIn,λ∈R{displaystyle lambda {mathsf {I}}_{n},,lambda in mathbb {R} }的矩阵(称为数乘矩阵)。其中的In{displaystyle {mathsf {I}}_{n}}是单位矩阵,也就是主对角线上的元素为1,其它元素为0的矩阵。任意矩阵M{displaystyle mathbf {M} }乘以单位矩阵都得到自身:MIn=M=InM{displaystyle mathbf {M} {mathsf {I}}_{n}=mathbf {M} ={mathsf {I}}_{n}mathbf {M} }。
除了最常见的矩阵乘法定义以外,也有一些较不常见的矩阵乘法,比如阿达马乘积和克罗内克乘积[18]。
线性方程组
矩阵乘法的一个基本应用是在线性方程组上。线性方程组是方程组的一种,它符合以下的形式:
- {a1,1x1+a1,2x2+⋯+a1,nxn=b1a2,1x1+a2,2x2+⋯+a2,nxn=b2⋮⋮am,1x1+am,2x2+⋯+am,nxn=bm{displaystyle {begin{cases}a_{1,1}x_{1}+a_{1,2}x_{2}+cdots +a_{1,n}x_{n}=b_{1}\a_{2,1}x_{1}+a_{2,2}x_{2}+cdots +a_{2,n}x_{n}=b_{2}\vdots quad quad quad vdots \a_{m,1}x_{1}+a_{m,2}x_{2}+cdots +a_{m,n}x_{n}=b_{m}end{cases}}}
其中的a1,1,a1,2{displaystyle a_{1,1},,a_{1,2}}以及b1,b2{displaystyle b_{1},,b_{2}}等等是已知的常数,而x1,x2{displaystyle x_{1},,x_{2}}等等则是要求的未知数。运用矩阵的方式,可以将线性方程组写成一个向量方程:
- Ax=b{displaystyle mathbf {A} mathbf {x} =mathbf {b} }
其中,A{displaystyle mathbf {A} }是由方程组里未知量的系数排成的m×n{displaystyle mtimes n}矩陣,x{displaystyle mathbf {x} }是含有n{displaystyle n}个元素的行向量,b{displaystyle mathbf {b} }是含有m{displaystyle m}个元素的行向量[19]。
- A=[a1,1a1,2⋯a1,na2,1a2,2⋯a2,n⋮⋮⋱⋮am,1am,2⋯am,n],x=[x1x2⋮xn],b=[b1b2⋮bm]{displaystyle mathbf {A} ={begin{bmatrix}a_{1,1}&a_{1,2}&cdots &a_{1,n}\a_{2,1}&a_{2,2}&cdots &a_{2,n}\vdots &vdots &ddots &vdots \a_{m,1}&a_{m,2}&cdots &a_{m,n}end{bmatrix}},quad mathbf {x} ={begin{bmatrix}x_{1}\x_{2}\vdots \x_{n}end{bmatrix}},quad mathbf {b} ={begin{bmatrix}b_{1}\b_{2}\vdots \b_{m}end{bmatrix}}}
这个写法下,将原来的多个方程转化成一个向量方程,在已知矩阵A{displaystyle mathbf {A} }和向量b{displaystyle mathbf {b} }的情况下,求未知向量x{displaystyle mathbf {x} }。
线性变换
矩陣是线性变换的便利表達法。矩陣乘法的本质在联系到线性变换的时候最能体现,因为矩阵乘法和线性变换的合成有以下的联系:
以Rn{displaystyle mathbb {R} ^{n}}表示所有長度為n{displaystyle n}的行向量的集合。每个m×n{displaystyle mtimes n}的矩阵A{displaystyle mathbf {A} }都代表了一个从Rn{displaystyle mathbb {R} ^{n}}射到Rm{displaystyle mathbb {R} ^{m}}的线性变换。反过来,对每個线性变换f:Rn→Rm{displaystyle f:mathbb {R} ^{n}rightarrow mathbb {R} ^{m}},都存在唯一m×n矩陣Af{displaystyle mathbf {A} _{f}}使得对所有Rn{displaystyle mathbb {R} ^{n}}中的元素x{displaystyle x},f(x)=Afx{displaystyle f(x)=A_{f}x}。这个矩阵Af{displaystyle mathbf {A} _{f}}第i{displaystyle i}行第j{displaystyle j}列上的元素是正则基向量ej=(0,⋯,0,1,0,⋯0)T{displaystyle mathbf {e} _{j}=(0,cdots ,0,1,0,cdots 0)^{T}}(第j个元素是1,其余元素是0的向量)在f{displaystyle f}映射后的向量f(ej){displaystyle f(mathbf {e} _{j})}的第i{displaystyle i}个元素。
也就是说,从Rn{displaystyle mathbb {R} ^{n}}射到Rm{displaystyle mathbb {R} ^{m}}的线性变换构成的向量空间L(Rn,Rm){displaystyle {mathcal {L}}left(mathbb {R} ^{n},mathbb {R} ^{m}right)}上存在一个到M(m,n,R){displaystyle {mathcal {M}}(m,n,mathbb {R} )}的一一映射:f↦Af{displaystyle fmapsto A_{f}}
以下是一些典型的2维实平面上的线性变换对平面向量(图形)造成的效果,以及它们对应的2维矩阵。其中每个线性变换将蓝色图形映射成绿色图形;平面的原点(0, 0)用黑点表示。
推移, 幅度m=1.25. | 水平鏡射变换 | “挤压”变换, 压缩程度r=3/2 | 伸縮,3/2倍 | 旋轉,左转30° |
[11.2501]{displaystyle {begin{bmatrix}1&1.25\0&1end{bmatrix}}} | [−1001]{displaystyle {begin{bmatrix}-1&0\0&1end{bmatrix}}} | [320023]{displaystyle {begin{bmatrix}{frac {3}{2}}&0\0&{frac {2}{3}}end{bmatrix}}} | [320032]{displaystyle {begin{bmatrix}{frac {3}{2}}&0\0&{frac {3}{2}}end{bmatrix}}} | [cos(π6)−sin(π6)sin(π6)cos(π6)]{displaystyle {begin{bmatrix}cos({frac {pi }{6}})&-sin({frac {pi }{6}})\sin({frac {pi }{6}})&cos({frac {pi }{6}})end{bmatrix}}} |
 |  |  |  |  |
设有k×m{displaystyle ktimes m}的矩陣B{displaystyle mathbf {B} }代表綫性變換g:Rm→Rk{displaystyle g:mathbf {R} ^{m}rightarrow mathbf {R} ^{k}},則矩陣積BA{displaystyle mathbf {BA} }代表了綫性變換的复合g∘f{displaystyle gcirc f}[20],因为
- (g∘f)(x)=g(f(x))=g(Ax)=B(Ax)=(BA)x{displaystyle (gcirc f)(x)=g(f(x))=g(mathbf {Ax} )=mathbf {B} (mathbf {Ax} )=(mathbf {BA} )mathbf {x} }
矩阵的秩是指矩阵中线性无关的行(列)向量的最大个数[21],同时也是矩阵对应的线性变换的像空间的维度[22]。秩-零化度定理说明矩阵的列数量等于矩阵的秩与零空间维度之和[23]。
方块矩阵
行数与列数相同的矩阵称为方块矩阵,简称方阵。所有n{displaystyle n}维的方块矩阵构成一个线性空间,这个空间对矩阵乘法也是封闭的,因此也是一个代数。方阵A{displaystyle mathbf {A} }称为可逆或非奇异的,如果存在另一个方阵B{displaystyle mathbf {B} },使得
- AB=In{displaystyle mathbf {AB} =mathbf {I} _{n}}
成立。这时候可以证明也有BA=In{displaystyle mathbf {BA} =mathbf {I} _{n}}成立[24],可将矩阵B{displaystyle mathbf {B} }称为A{displaystyle mathbf {A} }的逆矩阵[25]。一个矩阵A{displaystyle mathbf {A} }的逆矩阵如果存在的话,就是唯一的,通常记作A−1{displaystyle mathbf {A} ^{-1}}。
矩阵A{displaystyle mathbf {A} }的元素Ai,j{displaystyle A_{i,j}}称为其主对角线上的元素。方块矩阵A{displaystyle mathbf {A} }的所有主对角线元素之和称为它的迹,写作tr(A){displaystyle mathrm {tr} (mathbf {A} )}。尽管矩阵的乘法不满足交换律,方阵相乘时交换顺序会导致乘积变化,但它们的迹不会变,即tr(AB)=tr(BA){displaystyle mathrm {tr} (mathbf {AB} )=mathrm {tr} (mathbf {BA} )}[26]。除此以外,矩阵转置的迹等于其自身的迹,tr(A)=tr(AT){displaystyle mathrm {tr} (mathbf {A} )=mathrm {tr} (mathbf {A} ^{mathrm {T} })}。
如果一个方阵只有主对角线上的元素不是0,其它都是0,那么称其为对角矩阵。如果主对角线上方的元素都是0,那么称为下三角矩阵;反之如果主对角线下方的元素都是0,那么称为上三角矩阵。例如n=3{displaystyle n=3}的时候,这些矩阵分别写作:
[d11000d22000d33]{displaystyle {begin{bmatrix}d_{11}&0&0\0&d_{22}&0\0&0&d_{33}\end{bmatrix}}}(对角矩阵),[l1100l21l220l31l32l33]{displaystyle {begin{bmatrix}l_{11}&0&0\l_{21}&l_{22}&0\l_{31}&l_{32}&l_{33}\end{bmatrix}}}(下三角矩阵)和[u11u12u130u22u2300u33]{displaystyle {begin{bmatrix}u_{11}&u_{12}&u_{13}\0&u_{22}&u_{23}\0&0&u_{33}\end{bmatrix}}}(上三角矩阵)。
行列式

R2里的一个线性变换f将蓝色图形变成绿色图形,面积不变,而顺时针排布的向量x1和x2的变成了逆时针排布。对应的矩阵行列式是-1.
方块矩阵A{displaystyle mathbf {A} }的行列式是一个将其映射到标量的函数,记作det(A){displaystyle det(mathbf {A} )}或A{displaystyle mathbf {A} },反映了矩阵自身的一定特性。一个方阵的行列式等于0当且仅当该方阵不可逆。系数是实数的时候,二维(三维)方阵A{displaystyle mathbf {A} }的行列式的绝对值表示单位面积(体积)的图形经过A{displaystyle mathbf {A} }对应的线性变换后得到的图形的面积(体积),而它的正负则代表了对应的线性变换是否改变空间的定向:行列式为正说明它保持空间定向,行列式为负则说明它逆转空间定向。
2×2矩阵的行列式是
det(abcd)=ad−bc{displaystyle det {begin{pmatrix}a&b\c&dend{pmatrix}}=ad-bc}。
3×3矩阵的行列式由6项组成。更高维矩阵的行列式则可以使用莱布尼兹公式写出[27],或使用拉普拉斯展开由低一维的矩阵行列式递推得出[28]。
两个矩阵相乘,乘积的行列式等于它们的行列式的乘积:det(AB)=det(A)⋅det(B){displaystyle det(mathbf {AB} )=det(mathbf {A} )cdot det(mathbf {B} )}[29]。将矩阵的一行(列)乘以某个系数加到另一行(列)上不改变矩阵的行列式,将矩阵的两行(列)互换则使得其行列式变号[30]。用这两种操作可以将矩阵变成一个上三角矩阵或下三角矩阵,而后两种矩阵的行列式就是主对角线上元素的乘积,因此能方便地计算。运用行列式可以计算线性方程组的解(见克萊姆法則)[31]。
特征值与特征向量
n×n{displaystyle ntimes n}的方块矩阵A{displaystyle mathbf {A} }的一个特征值和对应特征向量是满足
Av=λv{displaystyle mathbf {Av} =lambda mathbf {v} }[32]的标量λ{displaystyle lambda }以及非零向量v{displaystyle mathbf {v} }。特征值和特征向量的概念对研究线性变换很有帮助。一个线性变换可以通过它对应的矩阵在向量上的作用来可视化。一般来说,一个向量在经过映射之后可以变为任何可能的向量,而特征向量具有更好的性质[33]。假设在给定的基底下,一个线性变换对应着某个矩阵A{displaystyle mathbf {A} },如果一个向量x{displaystyle mathbf {x} }可以写成矩阵的几个特征向量的线性组合:- x=c1xλ1+c2xλ2+⋯+ckxλk{displaystyle mathbf {x} =c_{1}mathbf {x} _{lambda _{1}}+c_{2}mathbf {x} _{lambda _{2}}+cdots +c_{k}mathbf {x} _{lambda _{k}}}
其中的xλi{displaystyle mathbf {x} _{lambda _{i}}}表示此向量对应的特征值是λi{displaystyle lambda _{i}},那么向量x{displaystyle mathbf {x} }经过线性变换后会变成:
- Ax=c1λ1xλ1+c2λ2xλ2+⋯+ckλkxλk{displaystyle mathbf {Ax} =c_{1}lambda _{1}mathbf {x} _{lambda _{1}}+c_{2}lambda _{2}mathbf {x} _{lambda _{2}}+cdots +c_{k}lambda _{k}mathbf {x} _{lambda _{k}}}
可以清楚地知道变换后向量的结构。
另一个等价的特征值定义是:标量λ{displaystyle lambda }为特征值,如果矩阵A−λIn{displaystyle mathbf {A} -lambda {mathsf {I}}_{n}}是不可逆矩阵。根据不可逆矩阵的性质,这个定义也可以用行列式方程描述:λ{displaystyle lambda }为特征值,如果
det(λIn−A)=0. {displaystyle det(lambda {mathsf {I}}_{n}-mathbf {A} )=0. }[34]这个定义中的行列式可以展开成一个关于λ{displaystyle lambda }的n阶多项式,叫做矩阵A的特征多项式,记为pA{displaystyle p_{mathbf {A} }}。特征多项式是一个首一多项式(最高次项系数是1的多项式)。它的根就是矩阵A{displaystyle mathbf {A} }特征值[35]。哈密尔顿-凯莱定理说明,如果用矩阵A{displaystyle mathbf {A} }本身代替多项式中的不定元λ{displaystyle lambda },那么多项式的值是零矩阵[36]:
pA(A)=0{displaystyle p_{mathbf {A} }(mathbf {A} )=0}。
对称
转置等于自己的矩阵,即满足A=AT{displaystyle mathbf {A} =mathbf {A} ^{mathrm {T} }}的方块矩阵A{displaystyle mathbf {A} }叫做对称矩阵。满足A=−AT{displaystyle mathbf {A} =-mathbf {A} ^{mathrm {T} }}的矩阵称为反对称矩阵。在复系数矩阵中,则有埃尔米特矩阵的概念:满足A=A∗{displaystyle mathbf {A} =mathbf {A} ^{*}}的方块矩阵称为埃尔米特矩阵,其中的A∗{displaystyle mathbf {A} ^{*}}表示A{displaystyle mathbf {A} }的共轭转置矩阵。
根据谱定理,实对称矩阵和复埃尔米特矩阵拥有特征基,即由矩阵的特征向量组成的基底。因此任何向量都能表示成矩阵特征向量的线性组合。此外,这两类矩阵的特征值都是实数[37]。
正定性
| 矩阵表达式 | [1400−14]{displaystyle {begin{bmatrix}{frac {1}{4}}&0\0&-{frac {1}{4}}end{bmatrix}}} | [140014]{displaystyle {begin{bmatrix}{frac {1}{4}}&0\0&{frac {1}{4}}end{bmatrix}}} |
| 正定性 | 不定矩阵 | 正定矩阵 |
| 对应二次型 | Q(x,y)=14(x2−y2){displaystyle Q(x,y)={frac {1}{4}}(x^{2}-y^{2})} | Q(x,y)=14(x2+y2){displaystyle Q(x,y)={frac {1}{4}}(x^{2}+y^{2})} |
| 取值图像 |  | |
| 说明 | 正定矩阵对应的二次型的取值范围永远是正的, 不定矩阵对应的二次型取值则可正可负 | |
n×n{displaystyle ntimes n}的实对称矩阵A{displaystyle mathbf {A} }如果满足对所有非零向量x∈Rn{displaystyle mathbf {x} in mathbf {R} ^{n}},对应的二次型
- Q(x)=xTAx{displaystyle Q(mathbf {x} )=mathbf {x} ^{mathrm {T} }mathbf {Ax} }
函数值都是正数,就称A{displaystyle mathbf {A} }为正定矩阵。类似地还有半正定矩阵、负定矩阵、不定矩阵等概念[38]。对称矩阵的正定性与其特征值密切相关。矩阵是正定的当且仅当其特征值都是正数[39]。
矩阵的计算
矩阵在许多学科领域中都有应用,在很多时候,除了需要知道矩阵的理论性质以外,还需要计算矩阵的数值。为了矩阵的计算能够足够精确与快捷,数值线性代数中专门有研究矩阵的数值计算方法[40]。与其它的数值计算一样,矩阵的数值计算注重的主要也是算法的复杂度和数值稳定性。矩阵的数值计算可以使用直接计算,也可以用迭代算法,例如在计算方块矩阵的特征值时,可以从一个非零向量x0{displaystyle x_{0}}开始,通过特定迭代方法得到一个逼近某个特征向量的向量序列[41]。
测量一个算法的复杂度是指估计此算法需要的基本运算如数字的加法和乘法的次数,或者找出它的一个上界。例如按照定义计算的话,两个n{displaystyle n}阶方阵的乘法需要n3{displaystyle n^{3}}次数字乘法计算,因为其乘积是一个n{displaystyle n}阶方阵,有n2{displaystyle n^{2}}个元素,计算每个元素需要n{displaystyle n}次数字乘法。如果使用施特拉森算法的话,可以将数字乘法的次数减低到大约n2.8{displaystyle n^{2.8}}次[42]。此外,编程语言或环境本身对算法的复杂度也会有影响。
某些特殊类型的矩阵携带的数据量比一般矩阵要少,同时带来的信息量比一般矩阵多。一个重要的例子是稀疏矩阵,这类矩阵中绝大部分的元素是零。有关稀疏矩阵的计算,如计算稀疏矩阵A{displaystyle mathbf {A} }的线性方程组Ax=b{displaystyle mathbf {Ax} =mathbf {b} }时,可以使用一些专用于稀疏矩阵的特殊算法(比如共轭梯度法[43]),减低计算复杂度。
算法的数值稳定性是指输入值的小变化不会让计算结果产生很大偏差。例如计算矩阵的逆时,可以用以下的算法(其中adj(A){displaystyle mathrm {adj} (mathbf {A} )}表示A{displaystyle mathbf {A} }的伴随矩阵)
- A−1=Adj(A)det(A){displaystyle mathbf {A} ^{-1}={frac {operatorname {Adj} (mathbf {A} )}{det(mathbf {A} )}}}
这个算法在A{displaystyle mathbf {A} }的行列式接近0的时候会引起很大的舍入误差[44]。而如果使用全选主元的高斯消去法求逆,则在复杂度降低的同时能够避免舍入误差,保证数值稳定性。
矩阵分解
矩阵研究的一大方向是将一般的矩阵用一些比较“简单”的矩阵来表示。这种表示方式称为矩阵的变换与分解。矩阵变换与分解的方法有很多,它们的目的都是希望化简后的矩阵保持原矩阵的某些性质,比如行列式、秩或逆矩阵,而形式相对简单,因而能用容易地进行讨论和计算,或者能使得某些算法更易执行。
LU分解将矩阵分解为一个下三角矩阵L{displaystyle mathbf {L} }和一个上三角矩阵U{displaystyle mathbf {U} }的乘积[45]。分解后的矩阵可以方便某些问题的解决。例如解线性方程组时,如果将系数矩阵A{displaystyle mathbf {A} }分解成A=LU{displaystyle mathbf {A} =mathbf {LU} }的形式,那么方程的求解可以分解为求解Ly=b{displaystyle mathbf {Ly} =mathbf {b} }和Ux=y{displaystyle mathbf {Ux} =mathbf {y} }两步,而后两个方程可以十分简洁地求解(详见三角矩阵中“向前与向后替换”一节)。又例如在求矩阵的行列式时,如果直接计算一个矩阵A{displaystyle mathbf {A} }的行列式,需要计算大约(n+1)!{displaystyle (n+1)!}次加法和乘法;而如果先对矩阵做LU{displaystyle mathbf {LU} }分解,再求行列式,就只需要大约n3{displaystyle n^{3}}次加法和乘法,大大降低了计算次数。这是因为做LU{displaystyle mathbf {LU} }分解的复杂度大约是n3{displaystyle n^{3}}次,而后注意到L{displaystyle mathbf {L} }和U{displaystyle mathbf {U} }是三角矩阵,所以求它们的行列式只需要将主对角线上元素相乘即可。

若尔当矩阵,其中灰色框内的是若尔当块
高斯消去法也是一种矩阵分解方法。通过初等变换操作,可以将任何矩阵变为阶梯形矩阵,而每个操作可以看做是将矩阵乘上一个特定的初等矩阵[46]。奇异值分解则是另一种分解方法,将一个矩阵表示成3个矩阵的乘积:A=UDV{displaystyle mathbf {A} =mathbf {UDV} }。其中U{displaystyle mathbf {U} }和V{displaystyle mathbf {V} }是酉矩阵,D{displaystyle mathbf {D} }是对角矩阵。
特征分解是将一个矩阵A{displaystyle mathbf {A} }写成PDP−1{displaystyle mathbf {PDP} ^{-1}}的形式,其中P{displaystyle mathbf {P} }是一个可逆矩阵,D{displaystyle mathbf {D} }是对角矩阵[47]。如果A{displaystyle mathbf {A} }的特征分解存在,就称它是可对角化的矩阵。不能对角化的矩阵,也有类似的分解方式。任意的矩阵A{displaystyle mathbf {A} }都可以写成PJP−1{displaystyle mathbf {PJP} ^{-1}}的形式,其中的矩阵J{displaystyle mathbf {J} }是若尔当标准型。若尔当标准型是矩阵的一种,它与对角矩阵类似,只不过主对角线上的元素不是数值,而是若尔当块:主对角线上为同一元素λi{displaystyle lambda _{i}},主对角线右上一行的次对角线上都是1,其它元素都是0的矩阵(见右图)[48]。特征分解可以方便计算矩阵的幂次和多项式,如要计算An{displaystyle mathbf {A} ^{n}}:
- An=(PDP−1)n=PDP−1PDP−1…PDP−1=PDnP−1{displaystyle mathbf {A} ^{n}=(mathbf {PDP} ^{-1})^{n}=mathbf {PDP} ^{-1}mathbf {PDP} ^{-1}ldots mathbf {PDP} ^{-1}=mathbf {PD} ^{n}mathbf {P} ^{-1}}
而其中对角矩阵的幂次Dn{displaystyle mathbf {D} ^{n}}要比An{displaystyle mathbf {A} ^{n}}容易计算得多。同理还可计算矩阵指数:eA{displaystyle e^{mathbf {A} }}(在线性微分方程中有应用)、矩阵对数和矩阵的平方根[49]。为了提高算法的数值稳定性,还有舒尔分解等矩阵分解方法[50]。
矩阵的推广
矩阵的元素除了可以是实数和复数以外,也可以任意环或域中元素。在线性代数中,矩阵的性质可以经由有限维的线性空间中的线性变换定义。更广泛的,无限维空间中的线性算子,则可以定义更广泛的无穷维矩阵。矩阵的另一种推广是张量。标量可以看成零维方式排列的数据(只有一个“点”),向量可以看成是一维方式排列的数据(若干个“点”排成的“线段”),矩阵可以看成是二维方式排列的数据(若干个“线段”排成的“矩形”),而张量的概念则包括了这几种排列方式。在张量的概念中,标量是零维张量,向量是一维张量,矩阵是二维張量,而更高维方式排列的数据方式就是高维张量[51]。
一般域和环上的矩阵
矩阵的元素除了可以是实数和复数以外,还可以是任何能够使得矩阵的运算律成立的元素。首先,矩阵的元素可以是任意一个域(即能够进行“加减乘除”运算的集合)中元素。例如编码理论中会出现系数为有限域中元素的矩阵,以及有理数系数的矩阵。如果矩阵的系数所在域K{displaystyle mathbf {K} }不是代数闭域,那么在求矩阵的特征值时,由于特征值是相应的特征多项式的根,可能不在系数域K{displaystyle mathbf {K} }中,而是在系数域的某个扩域L中。反过来,如果考虑扩域L/K{displaystyle mathbf {L/K} },以及L{displaystyle mathbf {L} }中的一个元素α{displaystyle alpha },以及L{displaystyle mathbf {L} }中线性变换mα:x↦αx{displaystyle m_{alpha }:,xmapsto alpha x},那么由于mα{displaystyle m_{alpha }}也是一个K{displaystyle mathbf {K} }-线性变换,它可以表示成一个n×n{displaystyle ntimes n}的K{displaystyle mathbf {K} }系数矩阵Xα{displaystyle X_{alpha }},其中的n{displaystyle n}是扩域L/K{displaystyle mathbf {L/K} }的阶数。α{displaystyle alpha }是这个矩阵的特征值,这个矩阵的特征多项式pXα{displaystyle p_{X_{alpha }}}是α{displaystyle alpha }在K{displaystyle mathbf {K} }中的最小多项式minK(α){displaystyle operatorname {min} _{mathbf {K} }(alpha )}的幂次:
pXα=(minK(α))r{displaystyle p_{X_{alpha }}=left(operatorname {min} _{mathbf {K} }(alpha )right)^{r},}。其中的r{displaystyle r}是扩域L/K{displaystyle mathbf {L/K} } (α){displaystyle (alpha )}的阶数[52]。
更一般的情况是矩阵的元素属于某个环R{displaystyle mathbf {R} }[53]。环是比域更广泛的概念,只要求其中元素能够进行加减法和乘法运算(不一定能定义除法)。给定一个环R{displaystyle mathbf {R} },M(m,n,R){displaystyle {mathcal {M}}(m,n,mathbf {R} )}中的矩阵之间可以相互加减以及相乘,所以M(m,n,R){displaystyle {mathcal {M}}(m,n,mathbf {R} )}关于矩阵的加法和乘法也构成一个环,称为矩阵环。n{displaystyle n}维方阵的环M(n,R){displaystyle {mathcal {M}}(n,mathbf {R} )}與左R{displaystyle mathbf {R} }-模Rn{displaystyle mathbf {R} ^{n}}的自同態環同構[54]。
若R{displaystyle mathbf {R} }是交换环,則M(m,R){displaystyle {mathcal {M}}(m,mathbf {R} )}是一个帶單位元的R{displaystyle mathbf {R} }-代數,满足结合律,但不满足交换律。其中的矩阵仍然可以用莱布尼兹公式定義行列式。一个矩阵可逆当且仅当其行列式为环R{displaystyle mathbf {R} }中的可逆元(域上的矩阵可逆只需行列式不等于0)[55]。
矩阵与线性变换
前面已经提到,所有Rn→Rm{displaystyle mathbf {R} ^{n}rightarrow mathbf {R} ^{m}}的线性变换都对应着一个M(m,n,R){displaystyle {mathcal {M}}(m,n,mathbf {R} )}中的矩阵。更一般地,给定了基底后,任意两个有限维线性空间之间的线性映射f:V→W{displaystyle f:mathbf {V} rightarrow mathbf {W} }也对应着一个矩阵Af=(aij){displaystyle mathbf {A} _{f}=(a_{ij})}。设空间V{displaystyle mathbf {V} }和W{displaystyle mathbf {W} }的基底分别是v1,…,vn{displaystyle mathbf {v} _{1},ldots ,mathbf {v} _{n}}和w1,…,wm{displaystyle mathbf {w} _{1},ldots ,mathbf {w} _{m}},那么
- 对任意 j=1,…,n{displaystyle j=1,ldots ,n},f(vj)=∑i=1mai,jwi{displaystyle f(mathbf {v} _{j})=sum _{i=1}^{m}a_{i,j}mathbf {w} _{i}}
矩阵Af{displaystyle mathbf {A} _{f}}实际上“记录”了V{displaystyle mathbf {V} }中每个基底向量经过变换后得到的W{displaystyle mathbf {W} }中的像在基底(w1,…,wm){displaystyle (mathbf {w} _{1},ldots ,mathbf {w} _{m})}下的形式。要注意矩阵的内容取决于基底的选择。可以说,矩阵是线性变换f在特定“角度”(基底)下的“素描”。不同的“角度”下,描述f{displaystyle f}的矩阵是不同的,但这些矩阵都是相似矩阵[56]。与矩阵有关的基本概念都可以用线性变换的层面来解释,比如一个矩阵的转置可以用f的对偶变换f∗:W∗→V∗{displaystyle f^{*}:mathbf {W} ^{*}rightarrow mathbf {V} ^{*}}来表示[57]。
当矩阵的元素是带单位元的环R{displaystyle mathbf {R} }中的元素时,m×n{displaystyle mtimes n}的R{displaystyle mathbf {R} }-矩阵对应的则是R{displaystyle mathbf {R} }-自由模Rm{displaystyle mathbf {R} ^{m}}和Rn{displaystyle mathbf {R} ^{n}}之间的R{displaystyle mathbf {R} }-线性变换。n=m{displaystyle n=m}的时候,这些R{displaystyle mathbf {R} }-线性变换可以相互复合,因此n{displaystyle n}维的R{displaystyle mathbf {R} }-矩阵环能够与R{displaystyle mathbf {R} }-自同态环Rn{displaystyle mathbf {R} ^{n}}同构。
矩阵群
群是比环更宽泛的代数结构,只需要集合配备一个满足结合律的二元运算,即将两个群内元素映射到群内一元素的运算。矩阵群是指矩阵关于矩阵乘法组成的群[58]。显然,只有方块矩阵才能构成乘法群。所有n{displaystyle n}维的可逆方阵构成一个群,称为n{displaystyle n}阶一般线性群。由于群内每个元素都必须是可逆的,任意的矩阵群都必然是一般线性群的子群。
能够在矩阵乘法和求逆矩阵运算下保持的性质都可以用来刻画一定的矩阵群。例如所有行列式为1的矩阵可以构成一个群,称为n{displaystyle n}阶特殊线性群[59]。所有n{displaystyle n}维的正交矩阵,即满足:
- MTM=I{displaystyle mathbf {M} ^{mathrm {T} }mathbf {M} =mathbf {I} }
的矩阵M{displaystyle mathbf {M} }也构成一个群,称为n{displaystyle n}阶正交群[60]。正交矩阵得名于它在Rn{displaystyle mathbf {R} ^{n}}中对应的线性变换具有保角性,也就是说对基本的点积,满足
(Mv)⋅(Mw)=v⋅w{displaystyle (mathbf {Mv} )cdot (mathbf {Mw} )=mathbf {v} cdot mathbf {w} }[61]
每个有限群都同构于一个矩阵群。实际上,每个有限群都同构于某个置换群的子群,而每个置换群都同构于一个矩阵群(见置换群的正则群表示[62])鉴于矩阵群的性质可以通过与矩阵相关的更多手段更好地理解,常常通过研究矩阵群来研究一个有限群。相关的理论称为群表示论。
无限维矩阵
无穷维矩阵可以指行数或列数无穷大,或两者都是无穷大的矩阵[63]。尽管这样的矩阵无法完整写出,但只要知道每行每列的元素的值,仍然可以对它进行矩阵操作和运算。这里矩阵的行数和列数甚至不一定需要是可数集。需要注意的是,无穷维矩阵的乘法涉及到无穷级数求和,因此只有在相关的无穷级数收敛的时候,才能定义矩阵的乘积[64]。无限维矩阵也可以是方块矩阵,定义为行标记集合与列标记集合相同的矩阵(如N×N{displaystyle mathbb {N} times mathbb {N} })[65]。
无限矩阵无法定义通常意义上的行列式,因此可逆矩阵不一定是方块矩阵,同理,酉矩阵也不一定要是方块矩阵[66]。
空矩阵
空矩阵是指行数或列数为零的矩阵。空矩阵的定义可以完善一些关于零维空间的约定。包括约定一个矩阵与空矩阵相乘得到的也是空矩阵,两个n×0{displaystyle ntimes 0}和0×p{displaystyle 0times p}的空矩阵相乘是一个n×p{displaystyle ntimes p}的零矩阵(所有元素都是零的矩阵)。0×0的空矩阵的行列式约定为1,所以它也可以有逆矩阵,约定为它自己[67]。
分塊矩陣
分塊矩陣是指一個大矩陣分割成“矩陣的矩陣”。舉例,以下的矩陣
- P=[1232127549266158]{displaystyle P={begin{bmatrix}1&2&3&2\1&2&7&5\4&9&2&6\6&1&5&8end{bmatrix}}}
可分割成4個2×2的矩陣
- P11=[1212],P12=[3275],P21=[4961],P22=[2658]{displaystyle P_{11}={begin{bmatrix}1&2\1&2end{bmatrix}},P_{12}={begin{bmatrix}3&2\7&5end{bmatrix}},P_{21}={begin{bmatrix}4&9\6&1end{bmatrix}},P_{22}={begin{bmatrix}2&6\5&8end{bmatrix}}}
P=[P11P12P21P22]{displaystyle P={begin{bmatrix}P_{11}&P_{12}\P_{21}&P_{22}end{bmatrix}}}。将矩阵分块可以使得矩阵结构清晰,在某些时候可以方便运算、证明。两个大小相同、分块方式也相同的矩阵可以相加。行和列的块数符合矩阵乘法要求时,分块矩阵也可以相乘。将矩阵分块相乘的结果与直接相乘是一样的。用分块矩阵求逆,可以将高阶矩阵的求逆转化为多次低阶矩阵的求逆[68]。
应用
矩阵在许多领域都应用广泛。有些时候用到矩阵是因为其表达方式紧凑,例如在博弈论和经济学中,会用收益矩阵来表示两个博弈对象在各种决策方式下的收益[69]。文本挖掘和索引典汇编的时候,比如在TF-IDF方法中,也会用到文件项矩阵来追踪特定词汇在多个文件中的出现频率[70]。
复数可以用实系数的2×2矩阵表示:
- a+ib↔[a−bba],{displaystyle a+ibleftrightarrow {begin{bmatrix}a&-b\b&aend{bmatrix}},}
这种表示法与复数的加减法、乘法都相兼容。比如,2×2的旋转矩阵可以用来表示模长为1的复数,一个向量乘以此旋转矩阵可以视作一个复数乘以该模长为1的复数。对四元数也有类似的矩阵表达[71]。
早期的密码技术如希尔密码也用到矩阵。然而,矩阵的线性性质使这类密码相对容易破解[72]。计算机图像处理也会用到矩阵来表示处理对象,并且用放射旋转矩阵来计算对象的变换,实现三维对象在特定二维屏幕上的投影[73]。多项式环上的矩阵在控制论中有重要作用。
化学中也有矩阵的应用,特别在使用量子理论讨论分子键和光谱的时候。具体例子有解罗特汉方程时用重叠矩阵和福柯矩阵来得到哈特里-福克方法中的分子轨道。
图论

一个无向图的邻接矩阵[110101010]{displaystyle {begin{bmatrix}1&1&0\1&0&1\0&1&0end{bmatrix}}}。
图论中可以用矩阵描述一个有限图[74]。这个矩阵叫做相关矩阵的邻接矩阵,记录了图的每两个顶点之间是否有边连接。对简单图来说,邻接矩阵的元素只取两个值:0和1,第i{displaystyle i}行第j{displaystyle j}列上取值为0,表示没有从第i{displaystyle i}个顶点连到第j{displaystyle j}个顶点的边,取值为1则说明有。如果是一般情况的话,第i{displaystyle i}行第j{displaystyle j} 列上的取值是从第i{displaystyle i}个顶点连到第j个顶点的边的数目。距离矩阵则是表示图中各顶点之间距离的矩阵[75]。在研究互联网等复杂网络的时候,邻接矩阵常常会是稀疏矩阵。因此网络理论中有专门研究稀疏矩阵的方面。
数学分析
在多元函数微积分学中,对二阶偏导数存在的函数f:Rn→R{displaystyle f:mathbf {R} ^{n}rightarrow mathbf {R} },可以定义其海森矩阵[76]:
H(f)(x)=[∂2f∂xi∂xj(x)]{displaystyle H(f)(x)=left[{frac {partial ^{2}f}{partial x_{i},partial x_{j}}}(x)right]}。

n=2{displaystyle n=2}时,海森矩阵[200−2]{displaystyle {begin{bmatrix}2&0\0&-2end{bmatrix}}}的特征值一正一负,说明函数f(x,y)=x2−y2{displaystyle f(x,y)=x^{2}-y^{2}}在(x=0,y=0){displaystyle (x=0,y=0)}处有一个鞍点(红色点)
严格来说,仅当函数在某一点上的二阶偏导数存在,才能定义这一点上的海森矩阵。海森矩阵给出了函数在这一点的变化率方面的信息。当给定的点x=(x1,…,xn){displaystyle mathbf {x} =(x_{1},ldots ,x_{n})}是函数平稳点(即函数f{displaystyle f}在这一点上的一阶偏导数∂f∂xi{displaystyle {frac {partial f}{partial x_{i}}}}都是0)时,就需要利用海森矩阵来查看函数在这一点周围的增长特性。多元函数在点x{displaystyle mathbf {x} }的泰勒展开是:
- f(x+h)=f(x)+∇f(x)⋅h+12hTH(f)(x)h+∘(‖x‖3){displaystyle f(x+h)=f(x)+nabla f(x)cdot h+{frac {1}{2}}h^{T}H(f)(x)h+circ left(|x|^{3}right)}
如果函数在点x的一阶偏导数都是0,那么∇f=0{displaystyle nabla f=0},所以函数在x附近的变化率取决于海森矩阵H(f)(x){displaystyle H(f)(x)}的性质。如果H(f)(x){displaystyle H(f)(x)}是正定矩阵,那么函数在点x取得局部最小值,如果是负定矩阵,则函数在x取得局部最大值。在这类情况下,关于函数f的条件最优化问题可以转变为关于海森矩阵的二次规划问题[77]。
矩阵在多元函数微积分中的另一个应用是雅可比矩阵。函数f:Rn→Rm{displaystyle f:mathbf {R} ^{n}rightarrow mathbf {R} ^{m}}在某一点x上的一阶偏导数存在时,可以定义它在这点上的雅可比矩阵[78]:
Jf(x)=[∂fi∂xj(x)]1≤i≤m,1≤j≤n{displaystyle J_{f}(x)=left[{frac {partial f_{i}}{partial x_{j}}}(x)right]_{1leq ileq m,1leq jleq n}}。如果n>m{displaystyle n>m},而Jf(x){displaystyle J_{f}(x)}又是满秩矩阵(秩等于m{displaystyle m})的话,根据反函数定理,可以找到函数f{displaystyle f}在x附近的一个局部的反函数[79]。
偏微分方程理论中,二阶拟线性偏微分方程可以根据最高次偏导项系数构成的矩阵的正定性分类。假设有一个二阶拟线性偏微分方程:
(E)∑1⩽i,j⩽naij∂2f∂xi∂xj+∑i=1nbi∂f∂xi+cf=g.{displaystyle (mathbf {E} )qquad qquad sum _{1leqslant i,jleqslant n}a_{ij}{frac {partial ^{2}f}{partial x_{i},partial x_{j}}}+sum _{i=1}^{n}b_{i}{frac {partial f}{partial x_{i}}}+cf=g.qquad } 并假设aij=aji,{displaystyle a_{ij}=a_{ji},}
记矩阵A=[aij]1⩽i,j⩽n{displaystyle mathbf {A} =left[a_{ij}right]_{1leqslant i,jleqslant n}}。如果矩阵A{displaystyle mathbf {A} }是正定或负定矩阵,那么就称方程(E){displaystyle (mathbf {E} )}为椭圆形偏微分方程;如果A{displaystyle mathbf {A} }不可逆,就称(E){displaystyle (mathbf {E} )}为抛物形偏微分方程,如果A{displaystyle mathbf {A} }可逆而且恰有n−1{displaystyle n-1}个特征值同号,就称(E){displaystyle (mathbf {E} )}为双曲型偏微分方程。其它情况下也称(E){displaystyle (mathbf {E} )}为超双曲形偏微分方程。不同类型的方程解的形式也不一样[80]。
用数值方法解偏微分方程时更需要用到矩阵。一个重要的方法是有限元方法,在求解各种物理中遇到的偏微分方程时广泛使用。有限元方法的基本思想是用一系列“简单”函数的线性组合来“逼近”偏微分方程的精确解。这些“简单”函数通常是指将求解区域分割成一定数量的“小块”后,仅在某一“小块”上非零的分段线性函数。选定了网格和“简单”函数后,可以求解关于刚度矩阵的方程得到近似解。有限元理论中证明了在满足一定的条件下,近似解将随着网格趋于精细而弱收敛到精确解[81][82]。
概率论与统计
概率论中常用到随机矩阵,即行向量是概率向量(即所有的元素都在0和1之间,并且加起来等于1的向量)的矩阵。随机矩阵可用来定义有限概率空间中的马尔可夫链。设随机变量Xn{displaystyle X_{n}}是某个马尔可夫链在t=n{displaystyle t=n}时刻的状态,所有可能的状态S={s1,s2,⋯,sm}{displaystyle S=left{s_{1},s_{2},cdots ,s_{m}right}}称为状态空间,那么随机矩阵Mnn+1{displaystyle M_{n}^{n+1}}则记录了假设已知Xn{displaystyle X_{n}}的可能情况下Xn+1{displaystyle X_{n+1}}做各种取值的可能性[83]。Mnn+1{displaystyle M_{n}^{n+1}}的第i{displaystyle i}行第j{displaystyle j}列上的元素表示当Xn=sj{displaystyle X_{n}=s_{j}}的时候,Xn+1=si{displaystyle X_{n+1}=s_{i}}的可能性。Mnn+1{displaystyle M_{n}^{n+1}}的第j{displaystyle j}行记录了从Xn=sj{displaystyle X_{n}=s_{j}}转移到Xn+1{displaystyle X_{n+1}}各种状态的可能性。所以Mnn+1{displaystyle M_{n}^{n+1}}叫做t=n{displaystyle t=n}时刻的转移矩阵。如果马尔可夫链的转移矩阵不随时刻变化,则称为齐次马尔可夫链。这时马尔可夫链的吸引态可以通过计算转移矩阵的特征向量得到[84]。
统计学中也会用到各种不同的矩阵。描述统计学中常常需要用矩阵的形式来描述数据样本,显得更为紧凑。几个随机变量的协方差矩阵表示它们之间的协方差关系,在某种程度上表示了它们相互间的关联程度(但不绝对)[85]。
统计学中用到矩阵的另一个地方是线性回归中的最小二乘法分析。当观测到随机样本(Yi,Xi1,…,Xip),i=1,…,n{displaystyle (Y_{i},X_{i1},ldots ,X_{ip}),,i=1,ldots ,n}时,线性回归法的目标是希望找到以下的线性关系:
- Yi=β0+β1Xi1+β2Xi2+…+βpXip+εi,i=1,…,n{displaystyle Y_{i}=beta _{0}+beta _{1}X_{i1}+beta _{2}X_{i2}+ldots +beta _{p}X_{ip}+varepsilon _{i},qquad i=1,ldots ,n}
即将变量Y{displaystyle mathbf {Y} }表示成X{displaystyle mathbf {X} }的分量的线性组合与一个已知的随机误差的和。这个表示可以写成矩阵的形式,并利用矩阵的奇异值分解来分析[86]。
另一种随机矩阵(random matrix)是指每个元素都是随机变量的矩阵,这些随机变量可以都遵循同一个分布,或各自遵循不同的分布。一个常见的例子是全部元素都是相互独立的标准正态分布随机变量的随机矩阵。这种随机矩阵在数论和物理中也有应用[87][88]。
物理学上的对称性及线性变换
线性变换及其所对应的对称,在现代物理学中有着重要的角色。例如,在量子场论中,基本粒子是由狭义相对论的洛伦兹群所表示,具体来说,即它们在旋量群下的表现。内含泡利矩阵及更通用的狄拉克矩阵的具体表示,在费米子的物理描述中,是一项不可或缺的构成部分,而费米子的表现可以用旋量来表述[89]。描述最轻的三种夸克时,需要用到一种内含特殊酉群SU(3)的群论表示;物理学家在计算时会用一种更简便的矩阵表示,叫盖尔曼矩阵,这种矩阵也被用作SU(3)规范群,而强核力的现代描述──量子色动力学的基础正是SU(3)。还有卡比博-小林-益川矩阵(CKM矩阵):在弱相互作用中重要的基本夸克态,与指定粒子间不同质量的夸克态不一样,但两者却是成线性关系,而CKM矩阵所表达的就是这一点[90]。
量子态的线性组合
1925年海森堡提出第一个量子力学模型时,使用了无限维矩阵来表示理论中作用在量子态上的算子[91]。这种做法在矩阵力学中也能见到。例如密度矩阵就是用来刻画量子系统中“纯”量子态的线性组合表示的“混合”量子态[92]。
另一种矩阵是用来描述构成实验粒子物理基石的散射实验的重要工具。当粒子在加速器中发生碰撞,原本没有相互作用的粒子在高速运动中进入其它粒子的作用区,动量改变,形成一系列新的粒子。这种碰撞可以解释为结果粒子状态和入射粒子状态线性组合的标量积。其中的线性组合可以表达为一个矩阵,称为S矩阵,其中记录了所有可能的粒子间相互作用[93]。
简正模式
矩阵在物理学中的另一类泛应用是描述线性耦合调和系统。这类系统的运动方程可以用矩阵的形式来表示,即用一个质量矩阵乘以一个广义速度来给出运动项,用力矩阵乘以位移向量来刻画相互作用。求系统的解的最优方法是将矩阵的特征向量求出(通过对角化等方式),称为系统的简正模式。这种求解方式在研究分子内部动力学模式时十分重要:系统内部由化学键结合的原子的振动可以表示成简正振动模式的叠加[94]。描述力学振动或电路振荡时,也需要使用简正模式求解[95]。
幾何光學
在幾何光學裏,可以找到很多需要用到矩陣的地方。幾何光學是一種忽略了光波波動性的近似理論,這理論的模型將光線視為幾何射線。採用近軸近似,假若光線與光軸之間的夾角很小,則透鏡或反射元件對於光線的作用,可以表達為2×2矩陣與向量的乘積。這向量的兩個分量是光線的幾何性質(光線的斜率、光線跟光軸之間在主平面的垂直距離)。這矩陣稱為光線傳輸矩陣,內中元素編碼了光學元件的性質。對於折射,這矩陣又細分為兩種:「折射矩陣」與「平移矩陣」。折射矩陣描述光線遇到透鏡的折射行為。平移矩陣描述光線從一個主平面傳播到另一個主平面的平移行為。
由一系列透鏡或反射元件組成的光學系統,可以很簡單地以對應的矩陣組合來描述其光線傳播路徑。[96]
電子學
在電子學裏,傳統的網目分析或節點分析會獲得一個線性方程組,這可以以矩陣來表示與計算。
很多種電子元件的電路行為可以用矩陣來描述。設定A{displaystyle A}為輸入向量,其兩個分量為輸入電壓v1{displaystyle v_{1}}與輸入電流i1{displaystyle i_{1}}。設定B{displaystyle B}為輸出向量,其兩個分量為輸出電壓v2{displaystyle v_{2}}與輸出電流i2{displaystyle i_{2}}。這電子元件的電路行為可以描述為B=H⋅A{displaystyle B=Hcdot A};其中,H{displaystyle H}是2×2矩陣,內有一個阻抗元素h12{displaystyle h_{12}}、一個導納元素h21{displaystyle h_{21}}、兩個無量綱元素h11{displaystyle h_{11}}與h22{displaystyle h_{22}}。這樣,電路的計算可以約化為矩陣計算。
参见
矩陣論專有名詞表:有關矩陣論所用到的名詞的定義- 方块矩阵
- 矩陣範數
- 雅可比矩阵
注释与参考
脚注
^ 1.01.11.21.3 董可荣 2007, 第3节
^ Shen, Crossley & Lun 1999
^ 克莱因 2002, 第33章第4节
^ Hawkins 1975
^ 克莱因 2002, 第33章第4节
^ The Collected Mathematical Papers of James Joseph Sylvester: 1837–1853, Paper 37, p. 247
^ 克莱因 2002, 第33章第4节
^ 克莱因 2002, 第33章第4节
^ Cayley 1889, vol. II, p. 475–496
^ Dieudonné, ed. 1978, Vol. 1, Ch. III, p. 96
^ 克莱因 2002, 第33章第4节
^ 克莱因 2002, 第33章第4节
^ 周建華. 《矩陣》. 台湾: 中央圖書出版社. 2002. ISBN 9789576374913 (中文).
^ Brown 1991, Definition I.2.1 (addition), Definition I.2.4 (scalar multiplication), and Definition I.2.33 (transpose)
^
Brown 1991, Theorem I.2.6
^ Brown 1991, Definition I.2.20
^ 林志兴 & 杨忠鹏 2010
^ Horn & Johnson 1985, Ch. 4 and 5
^ Brown 1991, I.2.21 and 22
^ Greub 1975, Section III.2
^ Brown 1991, Definition II.3.3
^ Greub 1975, Section III.1
^ Brown 1991, Theorem II.3.22
^ Brown 1991, Definition I.5.13
^ Brown 1991, Definition I.2.28
^ 这个结论容易从矩阵乘法的定义获得:
tr(AB)=∑i=1m∑j=1nAijBji=tr(BA){displaystyle scriptstyle operatorname {tr} ({mathsf {AB}})=sum _{i=1}^{m}sum _{j=1}^{n}A_{ij}B_{ji}=operatorname {tr} ({mathsf {BA}})}。
^ Brown 1991, Definition III.2.1
^ Mirsky 1990, Theorem 1.4.1
^ Brown 1991, Theorem III.2.12
^ Brown 1991, Corollary III.2.16
^ Brown 1991, Theorem III.3.18
^ Brown 1991, Definition III.4.1
^ Steven A. Leduc [[#CITEREFSteven A. Leduc|]], 第293页
^ Brown 1991, Definition III.4.9
^ Brown 1991, Corollary III.4.10
^ 王萼芳 1997, 4.2,定理3,第247页
^ Horn & Johnson 1985, Theorem 2.5.6
^ Horn & Johnson 1985, Chapter 7
^ Horn & Johnson 1985, Theorem 7.2.1
^ Bau III & Trefethen 1997
^ Householder 1975, Ch. 7
^ Golub & Van Loan 1996, Algorithm 1.3.1
^ Golub & Van Loan 1996, Chapters 9 and 10, esp. section 10.2
^ Golub & Van Loan 1996, Chapter 2.3
^ Press, Flannery & Teukolsky 1992
^ Stoer & Bulirsch 2002, Section 4.1
^ Horn & Johnson 1985, Theorem 2.5.4
^ Horn & Johnson 1985, Ch. 3.1, 3.2
^ Arnold & Cooke 1992, Sections 14.5, 7, 8
^ Bronson 1989, Ch. 15
^ Coburn 1955, Ch. V
^ Ash 2012, Chapter II
^ Lang 2002, Chapter XIII
^ Lang 2002, XVII.1, p. 643
^ Lang 2002, Proposition XIII.4.16
^ Greub 1975, Section III.3
^ Greub 1975, Section III.3.13
^ Baker 2003, Def. 1.30
^ Baker 2003, Theorem 1.2
^ Artin 1991, Chapter 4.5
^ Artin 1991, Theorem 4.5.13
^ Rowen 2008, Example 19.2, p. 198
^ Itõ, ed. 1987
^ Thankappan 1993
^ Thankappan 1993
^ Thankappan 1993
^ Faliva & Zoia 2008
^ 居余马 2002, 2.6
^ Fudenberg & Tirole 1983, Section 1.1.1
^ Manning 1999, Section 15.3.4
^ Ward 1997, Ch. 2.8
^ Stinson 2005, Ch. 1.1.5 and 1.2.4
^ Association for Computing Machinery 1979, Ch. 7
^ Godsil & Royle 2004, Ch. 8.1
^ Punnen 2002
^ Lang 1987a, Ch. XVI.6
^ Nocedal 2006, Ch. 16
^ Lang 1987a, Ch. XVI.1
^ Lang 1987a, Ch. XVI.5
^ Gilbarg & Trudinger 2001
^ Šolin 2005, Ch. 2.5
^ 伊泽尔莱斯 2005, Ch. 8
^ Latouche & Ramaswami 1999
^ Mehata & Srinivasan 1978, Ch. 2.8
^ Krzanowski 1988, Ch. 2.2., p. 60
^ Krzanowski 1988, Ch. 4.1
^ Conrey 2007
^ Zabrodin, Brezin & Kazakov et al. 2006
^
Itzykson & Zuber 1980, Ch. 2
^
见Burgess & Moore 2007, section 1.6.3. (SU(3)), section 2.4.3.2. (Kobayashi-Maskawa matrix)
^ Schiff 1968, Ch. 6
^ Bohm 2001, sections II.4 and II.8
^ Weinberg 1995, Ch. 3
^ Wherrett 1987, part II
^ Riley, Hobson & Bence 1997, 7.17
^ Guenther 1990, Ch. 5
参考文献
.mw-parser-output .refbegin{font-size:90%;margin-bottom:0.5em}.mw-parser-output .refbegin-hanging-indents>ul{list-style-type:none;margin-left:0}.mw-parser-output .refbegin-hanging-indents>ul>li,.mw-parser-output .refbegin-hanging-indents>dl>dd{margin-left:0;padding-left:3.2em;text-indent:-3.2em;list-style:none}.mw-parser-output .refbegin-100{font-size:100%}
Arnold, Vladimir I.; Cooke, Roger, Ordinary differential equations, Berlin, DE; New York, NY: Springer-Verlag, 1992, ISBN 978-3-540-54813-3
Artin, Michael, Algebra, Prentice Hall, 1991, ISBN 978-0-89871-510-1
Association for Computing Machinery, Computer Graphics, Tata McGraw–Hill, 1979, ISBN 978-0-07-059376-3
Baker, Andrew J., Matrix Groups: An Introduction to Lie Group Theory, Berlin, DE; New York, NY: Springer-Verlag, 2003, ISBN 978-1-85233-470-3
Bau III, David; Trefethen, Lloyd N., Numerical linear algebra, Philadelphia, PA: Society for Industrial and Applied Mathematics, 1997, ISBN 978-0-89871-361-9
Bretscher, Otto, Linear Algebra with Applications 3rd, Prentice Hall, 2005
王萼芳, 高等代数教程 第1版, 清华大学出版社, 1997, ISBN 9787302024521
Bronson, Richard, Schaum's outline of theory and problems of matrix operations, New York: McGraw–Hill, 1989, ISBN 978-0-07-007978-6
Brown, William A., Matrices and vector spaces, New York, NY: M. Dekker, 1991, ISBN 978-0-8247-8419-5
Coburn, Nathaniel, Vector and tensor analysis, New York, NY: Macmillan, 1955, OCLC 1029828
Conrey, J. Brian, Ranks of elliptic curves and random matrix theory, Cambridge University Press, 2007, ISBN 978-0-521-69964-8
Fudenberg, Drew; Tirole, Jean, Game Theory, MIT Press, 1983
Gilbarg, David; Trudinger, Neil S., Elliptic partial differential equations of second order 2nd, Berlin, DE; New York, NY: Springer-Verlag, 2001, ISBN 978-3-540-41160-4
Godsil, Chris; Royle, Gordon, Algebraic Graph Theory, Graduate Texts in Mathematics 207, Berlin, DE; New York, NY: Springer-Verlag, 2004, ISBN 978-0-387-95220-8
Golub, Gene H.; Van Loan, Charles F., Matrix Computations 3rd, Johns Hopkins, 1996, ISBN 978-0-8018-5414-9
Greub, Werner Hildbert, Linear algebra, Graduate Texts in Mathematics, Berlin, DE; New York, NY: Springer-Verlag, 1975, ISBN 978-0-387-90110-7
Guenther, Robert D., Modern Optics, John Wiley, 1990, ISBN 0-471-60538-7
Halmos, Paul Richard, A Hilbert space problem book, Graduate Texts in Mathematics 19 2nd, Berlin, DE; New York, NY: Springer-Verlag, 1982, ISBN 978-0-387-90685-0, MR 675952
Horn, Roger A.; Johnson, Charles R., Matrix Analysis, Cambridge University Press, 1985, ISBN 978-0-521-38632-6
Householder, Alston S., The theory of matrices in numerical analysis, New York, NY: Dover Publications, 1975, MR 0378371
Krzanowski, Wojtek J., Principles of multivariate analysis, Oxford Statistical Science Series 3, The Clarendon Press Oxford University Press, 1988, ISBN 978-0-19-852211-9, MR 969370
Itõ, Kiyosi (编), Encyclopedic dictionary of mathematics. Vol. I-IV 2nd, MIT Press, 1987, ISBN 978-0-262-09026-1, MR 901762
Ash, Robert B., A Course In Algebraic Number Theory (PDF), Dept. of Mathematics, University of Illinois
Lang, Serge, Analysis II, Addison-Wesley, 1969
Lang, Serge, Calculus of several variables 3rd, Berlin, DE; New York, NY: Springer-Verlag, 1987a, ISBN 978-0-387-96405-8
Lang, Serge, Linear algebra, Berlin, DE; New York, NY: Springer-Verlag, 1987b, ISBN 978-0-387-96412-6
Latouche, Guy; Ramaswami, Vaidyanathan, Introduction to matrix analytic methods in stochastic modeling 1st, Philadelphia, PA: Society for Industrial and Applied Mathematics, 1999, ISBN 978-0-89871-425-8
Manning, Christopher D.; Schütze, Hinrich, Foundations of statistical natural language processing, MIT Press, 1999, ISBN 978-0-262-13360-9
Mehata, K. M.; Srinivasan, S. K., Stochastic processes, New York, NY: McGraw–Hill, 1978, ISBN 978-0-07-096612-3
Mirsky, Leonid, An Introduction to Linear Algebra, Courier Dover Publications, 1990, ISBN 978-0-486-66434-7
Nocedal, Jorge; Wright, Stephen J., Numerical Optimization 2nd, Berlin, DE; New York, NY: Springer-Verlag: 449, 2006, ISBN 978-0-387-30303-1
Bohm, Arno, Quantum Mechanics: Foundations and Applications, Springer, 2001, ISBN 0-387-95330-2
Burgess, Cliff; Moore, Guy, The Standard Model. A Primer, Cambridge University Press, 2007, ISBN 0-521-86036-9
Guenther, Robert D., Modern Optics, John Wiley, 1990, ISBN 0-471-60538-7
Itzykson, Claude; Zuber, Jean-Bernard, Quantum Field Theory, McGraw–Hill, 1980, ISBN 0-07-032071-3
Riley, Kenneth F.; Hobson, Michael P.; Bence, Stephen J., Mathematical methods for physics and engineering, Cambridge University Press, 1997, ISBN 0-521-55506-X
Schiff, Leonard I., Quantum Mechanics 3rd, McGraw–Hill, 1968
Weinberg, Steven, The Quantum Theory of Fields. Volume I: Foundations, Cambridge University Press, 1995, ISBN 0-521-55001-7
Wherrett, Brian S., Group Theory for Atoms, Molecules and Solids, Prentice–Hall International, 1987, ISBN 0-13-365461-3
Zabrodin, Anton; Brezin, Édouard; Kazakov, Vladimir; Serban, Didina; Wiegmann, Paul, Applications of Random Matrices in Physics (NATO Science Series II: Mathematics, Physics and Chemistry), Berlin, DE; New York, NY: Springer-Verlag, 2006, ISBN 978-1-4020-4530-1
林志兴; 杨忠鹏, 与给定矩阵A的可交换子环C(A)的一些探讨, 莆田学院学报,2010年, 17(2), 2010
Oualline, Steve, Practical C++ programming, O'Reilly, 2003, ISBN 978-0-596-00419-4
Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T., LU Decomposition and Its Applications, Numerical Recipes in FORTRAN: The Art of Scientific Computing (PDF) 2nd, Cambridge University Press: 34–42, 1992, (原始内容 (PDF)存档于2009-09-06)
Punnen, Abraham P.; Gutin, Gregory, The traveling salesman problem and its variations, Boston, MA: Kluwer Academic Publishers, 2002, ISBN 978-1-4020-0664-7
Reichl, Linda E., The transition to chaos: conservative classical systems and quantum manifestations, Berlin, DE; New York, NY: Springer-Verlag, 2004, ISBN 978-0-387-98788-0
Rowen, Louis Halle, Graduate Algebra: noncommutative view, Providence, RI: American Mathematical Society, 2008, ISBN 978-0-8218-4153-2
Šolin, Pavel, Partial Differential Equations and the Finite Element Method, Wiley-Interscience, 2005, ISBN 978-0-471-76409-0
Stinson, Douglas R., Cryptography, Discrete Mathematics and its Applications, Chapman & Hall/CRC, 2005, ISBN 978-1-58488-508-5
Stoer, Josef; Bulirsch, Roland, Introduction to Numerical Analysis 3rd, Berlin, DE; New York, NY: Springer-Verlag, 2002, ISBN 978-0-387-95452-3
Ward, J. P., Quaternions and Cayley numbers, Mathematics and its Applications 403, Dordrecht, NL: Kluwer Academic Publishers Group, 1997, ISBN 978-0-7923-4513-8, MR 1458894
(中文)居余马; 林翠琴, 线性代数, 清华大学出版社, 2002, ISBN 978-7-302-06507-4
(中文)克莱因, 莫里斯; 著,张理京、张锦炎、江泽涵译, 《古今数学思想》第三卷, 上海科学技术出版社, 2002, ISBN 7-5323-6172-1
Wolfram, Stephen, The Mathematica Book 5th, Champaign, IL: Wolfram Media, 2003, ISBN 978-1-57955-022-6
Thankappan, V. K., Quantum Mechanics 2nd, New Age International, 1993, ISBN 9788122405262
Faliva, Mario; Zoia, Maria Grazia, Dynamic Model Analysis: Advanced Matrix Methods and Unit-Root Econometrics Representation Theorems 2nd, Berlin, DE; New York, NY: Springer-Verlag: 218, 2008, ISBN 9783540859956
伊泽尔莱斯, 刘晓艳,刘学深译, 微分方程数值分析基础教程, 清华大学出版社, 2005, ISBN 9787302106524
董可荣, 矩阵理论的历史研究, 《山东大学》, 2007
Bôcher, Maxime, Introduction to higher algebra, New York, NY: Dover Publications, 2004, ISBN 978-0-486-49570-5
Cayley, Arthur, The collected mathematical papers of Arthur Cayley, I (1841–1853), Cambridge University Press: 123–126, 1889
Dieudonné, Jean (编), Abrégé d'histoire des mathématiques 1700-1900, Paris, FR: Hermann, 1978
Hawkins, Thomas, Cauchy and the spectral theory of matrices, Historia Mathematica, 1975, 2: 1–29, ISSN 0315-0860, MR 0469635, doi:10.1016/0315-0860(75)90032-4
Knobloch, Eberhard, From Gauss to Weierstrass: determinant theory and its historical evaluations, The intersection of history and mathematics, Science Networks Historical Studies 15, Basel, Boston, Berlin: Birkhäuser: 51–66, 1994, MR 1308079
Kronecker, Leopold, Hensel, Kurt, 编, Leopold Kronecker's Werke, Teubner, 1897
Mehra, Jagdish; Rechenberg, Helmut, The Historical Development of Quantum Theory 1st, Berlin, DE; New York, NY: Springer-Verlag, 1987, ISBN 978-0-387-96284-9
Shen, Kangshen; Crossley, John N.; Lun, Anthony Wah-Cheung, Nine Chapters of the Mathematical Art, Companion and Commentary 2nd, Oxford University Press, 1999, ISBN 978-0-19-853936-0
Weierstrass, Karl, Collected works 3, 1915
外部链接
維基教科書中的相關電子教程:矩阵 |
- 百科全书
Hazewinkel, Michiel (编), Matrix, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4
- 历史
- MacTutor: Matrices and determinants
- Matrices and Linear Algebra on the Earliest Uses Pages
- Earliest Uses of Symbols for Matrices and Vectors
- 在线书籍
Kaw, Autar K., Introduction to Matrix Algebra, ISBN 978-0-615-25126-4
The Matrix Cookbook (PDF), [2014-93-24] 请检查|access-date=中的日期值 (帮助)
Brookes, Mike, The Matrix Reference Manual, London: Imperial College, 2005 [2008-12-10]
- 线上矩阵计算器
Matrix Calculator (DotNumerics)
Xiao, Gang, Matrix calculator, [2008-12-10]
Online matrix calculator, [2008-12-10]
Online matrix calculator (ZK framework), [2009-11-26], (原始内容存档于2013-05-12)
Oehlert, Gary W.; Bingham, Christopher, MacAnova, University of Minnesota, School of Statistics, [2008-12-10] , a freeware package for matrix algebra and statistics
Online matrix calculator, [2009-12-14]
- Operation with matrices in R (determinant, track, inverse, adjoint, transpose)
| ||||||||||||||
|




















![{displaystyle mathbf {A} _{[i,j]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a8b9bccc1ff7fa48155b222898cc3fb9c43765d)
![{displaystyle mathbf {A} _{[4,3]}=7}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fba467f70d1c016fd117fd51a76849b27a4bd4c9)
![{displaystyle mathbf {A} [mathbf {a} _{ij}]_{mtimes n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa318f257b9fd60354a292cfd27592f99d0396ed)
![{displaystyle mathbf {A} [mathbf {a} _{i,j}]_{mtimes n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/316e8349ed25764fab2380f419c980ef3a22fc33)
![{displaystyle mathbf {A} =left[f(i,j)right]_{mtimes n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec2f4f48113c05c6807bec3149c6e1faaf68d891)
![{displaystyle mathbf {B} =left[i+2jright]_{2times 3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/983a530d365d0e9b8cdbfb1eae041f89d403c6ac)


![{displaystyle mathbf {B} =left[i+2j+3right]_{2times 3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f2a9de3c58ca7990e946b699273dbbccec787e5)































![[mathbf{AB}]_{i,j} = A_{i,1}B_{1,j} + A_{i,2}B_{2,j} + cdots + A_{i,n}B_{n,j} = sum_{r=1}^n A_{i,r}B_{r,j}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db581eb370e44283170093b08a2ae8407bc38314)











































































































































![H(f)(x) = left[ frac {partial^2 f}{partial x_i , partial x_j}(x) right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b933754bfe181046375b707808338537bbb459a5)










![J_f(x) = left [frac {partial f_i}{partial x_j}(x) right ]_{1 leq i leq m, 1 leq j leq n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50fbeb6d77601ce7cde35e0d842e6af992c9ccf5)




![mathbf{A}=left[ a_{ij} right]_{1 leqslant i , j leqslant n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b3772f4e0a0e32adcf80e2c5c94496c1f60af43)
























